Страница 95, ГДЗ по математике за 4 класс к учебнику Моро часть 1
Страница 95
Краткое условие: Реши уравнения.
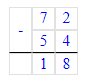
x=72-54
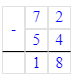
Ответ: x=18
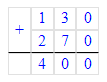
x÷8=130+270
x÷8=400
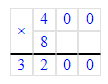
x=400∙8
x=3 200
Ответ: x=3 200.
400÷x=1 000÷10
400÷x=100
x=400÷100
x=4
Ответ: x=4.
x-290=470+230
x-290=700
x=700+290
x=990
Ответ: x=990.
x+320=90∙8
x+320=720
x=720-320
x=400
Ответ: x=400.
15∙x=630÷7
15∙x=90
x=90÷15
x=6
Ответ:x=6.
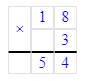
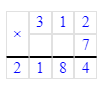
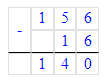
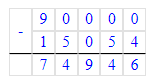
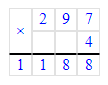
1) 72 - х = 18 · 3;
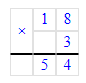
х = 72 - 54;
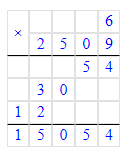
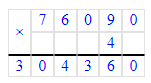
2) х : 8 = 130 + 270;
х = 400 · 8;
3) 400 : х = 1 000 : 10;
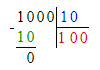
х = 400 : 100;
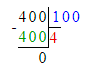
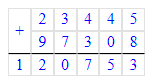
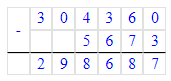
4) х - 290 = 470 + 230;
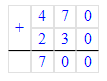
х = 700 + 290;
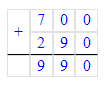
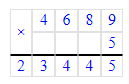
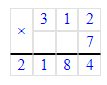
5) х + 320 = 90 · 8;
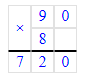
х = 720 - 320;
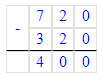
6) 15 · х = 630 : 7;
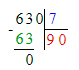
х = 90 : 15;
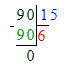
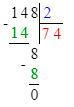
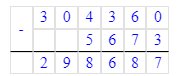
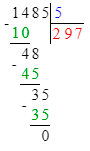
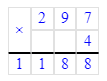
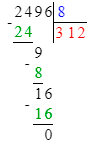
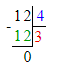
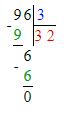
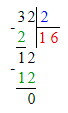
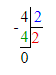
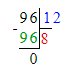
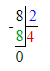
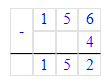
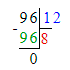
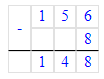
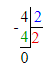
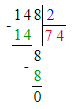
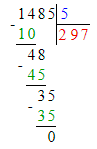
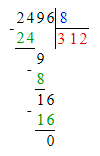
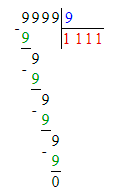
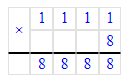
Краткое условие: Со 100 ульев собрали 2 т мёда. Сколько кг мёда собрали с 8 ульев, если со всех ульев собрали поровну?
8 ульев -? т мёда.
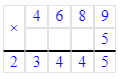
2) 20∙8=160 (кг)- мёда собрали с 8 ульев.
ШАГ 1. Найти сколько мёда собрали с 1 улья.
ШАГ 2. Найти сколько мёда собрали с 8 ульев.
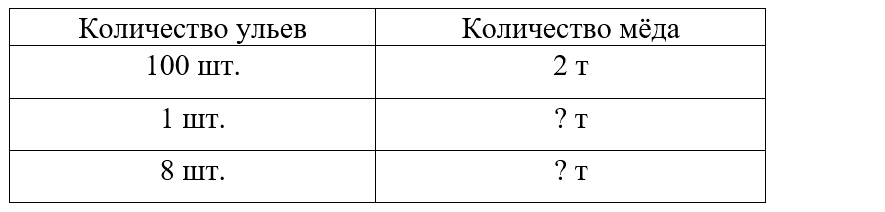
1) 2 т : 100 = 2 000 кг : 100 = 20 кг – с 1 улья
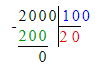
2) 20 · 8 = 160 кг – с 8 ульев
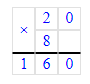
2) 20 · 8 = 160 (кг)
Ответ: с 8 ульев собрали 160 кг мёда.
Краткое условие: За день продали 6 чайных чашек по 100 р. и 10 кофейных, всего на 1 800 р. Сколько стоила кофейная чашка?

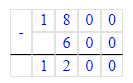
2) 1800-600=1 200 (р.)-получили за продажу 10 кофейных чашек;
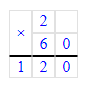
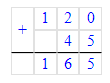
3)1 200÷10=120 (р.)- стоила кофейная чашка.
ШАГ 1. Найти стоимость 6 чайных чашек.
ШАГ 2. Найти стоимость 10 кофейных чашек.
ШАГ 3. Найти стоимость 1 кофейной чашки.

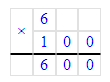
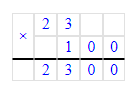
1) 6 · 100 = 600 р. – стоят 6 чайных чашек
2) 1 800 - 600 = 1 200 р. – стоят 10 кофейных чашек
3) 1 200 : 10 = 120 р. – стоит 1 кофейная чашка
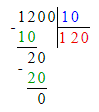
2) 1 800 - 600 = 1 200 (р.)
3) 1 200 : 10 = 120 (р.)
Ответ: 1 кофейная чашка стоит 120 р.
2 ч 45 мин=(2∙60) мин+45 мин=120 мин+45 мин=165 мин;
62 335 кг=62 т 335 кг;
584 мм=58 см 4 мм.
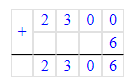
4) 584 мм = 58 см 4 мм;
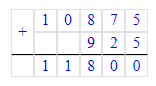
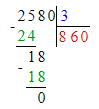
10 км 875 м = 10 875 м;

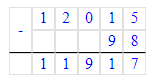
2) 12 т 015 кг – 98 кг = 11 т 917 кг;
12 т 015 кг = 12 015 кг;

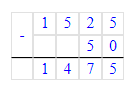
3) 15 м2 25 дм2 – 50 дм2 = 14 м2 75 дм2;
15 м2 25 дм2 = 1 525 дм2;

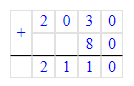
4) 20 дм2 30 см2 + 80 см2 = 21 дм2 10 см2;
20 дм2 30 см2 = 2 030 см2;

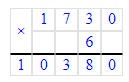
5) 17 м 30 см · 6 = 103 м 80 см;
17 м 30 см = 1 730 см;

6) 25 ц 80 кг : 3 = 8 ц 60 кг;
25 ц 80 кг = 2 580 кг;

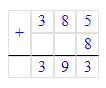
7) 38 см 5 мм + 8 мм = 39 см 3 мм;
38 см 5 мм = 385 мм;

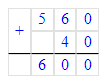
8) 5 м2 60 дм2 + 40 дм2 = 6 м2;
5 м2 60 дм2 = 560 дм2;

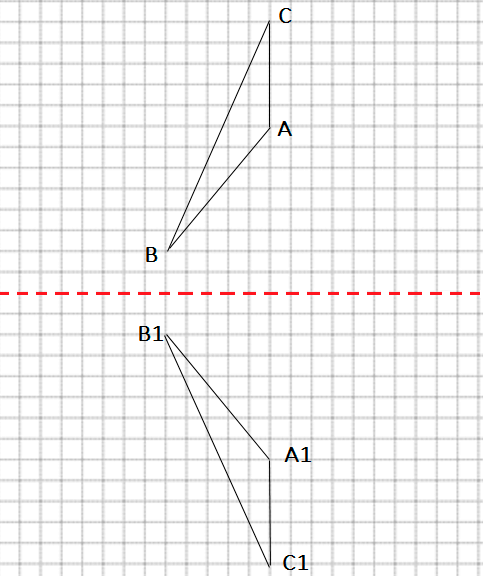
Краткое условие: 1) Рассмотри чертежи, выпиши отдельно тупые, острые и прямые углы. 2) Начерти фигуру, симметричную треугольнику ABC.
Острые углы: CBA, CDA, BCA, CAK, BAD, KAD, KAB.
Прямые углы: AKB, AKC.
2) Треугольник А1В1С1 симметричен треугольнику АВС.
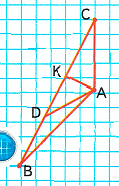
∠СAB; ∠ВDA; ∠DAC;
3) Выпишем отдельно названия острых углов:
∠KCA; ∠CAK; ∠KAD; ∠KDA; ∠KAB; ∠DAB; ∠ABD;
4) Выпишем отдельно названия прямых углов:
∠CKA; ∠DKA; ∠KAB;
5) Начертим фигуру, симметричную треугольнику АВС:

Краткое условие: Как называются числа и соответствующее выражение при умножении? при делении?
При делении: делимое ÷ делитель= частное.
При умножении числа и выражение называются следующим образом: первый множитель, второй множитель, произведение.
2) Подумаем, как называются числа и соответствующее выражение при делении:
При делении числа и выражение называются следующим образом: делимое, делитель, частное.
Краткое условие: Покажи на примере, как можно умножить сумму нескольких чисел на какое-либо число.
Пример: (20+15)∙3=20∙3+15∙3=60+45=105.
Чтобы умножить сумму нескольких чисел на какое-либо число, необходимо каждое слагаемое умножить на это число, а результат сложить.
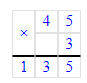
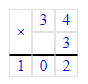
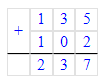
(45 + 34) · 3 = 45 · 3 + 34 · 3 = 135 + 102 = 237;
Краткое условие: Как можно разделить сумму на число: (36 + 24) : 6?
(36+24)÷6=60÷6=10;
(36+24)÷6=36÷6+24÷6=6+4=10.
Чтобы разделить сумму на число, можно каждое слагаемое разделить на это число, а результат сложить.
(36 + 24) : 6 = 36 : 6 + 24 : 6 = 6 + 4 = 10;
Краткое условие: Чему равно произведение, если множитель равен 0 или 1? Приведи примеры.
a∙0=0;0∙a=0.
При умножении любого числа (кроме нуля) на единицу получится само это число: b∙1=b;1∙b=b.
Примеры:
84∙0=0;0∙169=0;2 589∙1=2 589;1∙23 687=23 687.
Если один из множителей равен 0, то произведение равняется нулю.
2) Подумаем, чему равно произведение, если один из множителей равен 1:
Если один из множителей равен 1, то произведение равняется самому числу.
3) Приведём примеры:
1. 39 · 0 = 39;
2. 1 · 5 = 5;
Краткое условие: Чему равно частное при делителе 1 и при делимом 0?
a÷1=a.
Если делимое равно 0, то частное равно нулю:
0÷a=0.
Если делитель равен 1, то частное равняется делимому.
2) Подумаем, чему равно частное, если делимое равно 0:
Если делимое равно 0, то частное равняется нулю.
Краткое условие: Что получится, если произведение разделить на один из множителей?
7∙8=56;56÷8=7.
Если произведение двух чисел разделить на один из множителей, то получится второй множитель.
Краткое условие: Что получится при умножении делителя на частное и при делении делимого на частное?
15÷3=5;3∙5=15.
Если разделить делимое на частное, то получится делитель:
24÷4=6;24÷6=4.
Если умножить делитель на частное, то получится делимое.
2) Подумаем, что получится, если разделить делимое на частное:
Если разделить делимое на частное, то получится делитель.
Краткое условие: Как можно проверить умножение? деление?
Чтобы проверить деление, надо частное умножить на делитель и в результате получится делимое.
Чтобы проверить деление, надо делимое разделить на частное и в результате получится делитель.
Умножение нужно проверять делением.
2) Подумаем, как проверить деление:
Деление нужно проверять умножением.
Страница 95. Что узнали. Чему научились. Номер: 44, 45, 46, 47, 48, 49, 50, 1, 2, 3, 4, 5, 6, 7, 8, задача на полях.



