Страница 92, ГДЗ по математике за 4 класс к учебнику Моро часть 1
Страница 92
Краткое условие: Дима купил 4 игрушки по одинаковой цене, а Настя — 3 такие же. Все игрушки стоили 56 р.
Настя – 3 игрушки;
Стоимость-56 р.
56÷(3+4) - цена 1-й игрушки.
56÷(3+4)∙3 - столько рублей Настя заплатила за свои игрушки.
56÷(3+4)∙4 - столько рублей заплатил Дима за свои игрушки.
1) 3 + 4;
(данное выражение обозначает количество купленных игрушек);
2) 56 : (3 + 4);
(данное выражение обозначает цену одной игрушки);
3) 56 : (3 + 4) · 3;
(данное выражение обозначает стоимость купленных игрушек Настей);
4) 56 : (3 + 4) · 4;
(данное выражение обозначает стоимость купленных игрушек Димой);
Краткое условие: Мальчик купил 6 тетрадей в клетку и 5 в линейку по одинаковой цене, заплатив всего d р.
В линейку – 5 тетрадей;
Стоимость - d р.
6+5- столько тетрадей купил мальчик всего.
d÷(6+5)- цена одной тетради.
d÷(6+5)∙6- стоимость всех тетрадей в клетку.
1) 6 + 5;
(данное выражение обозначает количество купленных тетрадей);
2) d : (6 + 5);
(данное выражение обозначает цену одной тетради);
3) d : (6 + 5) · 6;
(данное выражение обозначает стоимость купленных тетрадей в клетку);
Краткое условие: В одном куске 5 м ткани, в другом 7 м такой же ткани. За оба куска заплатили к р.
2 кусок – 7м;
Стоимость –k р.
k÷(5+7)- цена 1 метра ткани.
k÷(5+7)∙5- стоимость 1-го куска ткани.
k÷(5+7)∙7- стоимость 2-го куска ткани.
1) k : (5 + 7);
(данное выражение обозначает цену 1 м ткани);
2) k : (5 + 7) · 5;
(данное выражение обозначает стоимость 5 м ткани);
3) k : (5 + 7) · 7;
(данное выражение обозначает стоимость 7 м ткани);
Краткое условие: Как, не изменяя чисел, сделать равенства верными?
78-(60÷2+4)=78-(30+4)=78-34=44.
1) (78 - 60) : 2 + 4 = 13;
2) 78 - (60 : 2 + 4) = 44;
Краткое условие: Во сколько раз 1 дм больше 1 мм, 1 ц больше 10 кг, 1 ч больше 10 мин, 1 км больше 100 м, 1 м² больше 1 см²?
100÷1=100 раз.
2) Так как 1 ц= 100 кг, то 1 ц больше 10 кг в:
100÷10=10 раз.
3) Так как 1 ч = 60 мин, то 1 ч больше 10 мин в :
60÷10=6 раз.
4) Так как 1 км= 1 000 м, то 1 км больше 100 м в :
1 000÷100=10 раз.
5) Так как 1 м2= 10 000 см2, то 1 м2 больше 1 см2 в:
10 000÷1=10 000 раз.
Так как 1 дм = 10 см, а 1 см = 10 мм, то 1 дм = 100 мм.
Следовательно, 1 дм больше, чем 1 мм в 100 раз.
2) Подумаем, во сколько раз 1 ц больше, чем 10 кг:
Так как 1 ц = 100 кг, а 100 : 10 = 10, значит, 1 ц больше, чем 10 кг в 10 раз.
3) Подумаем, во сколько раз 1 ч больше, чем 10 мин:
Так как 1 ч = 60 мин, а 60 : 10 = 6, значит, 1 ч больше, чем 10 мин в 6 раз.
4) Подумаем, во сколько раз 1 км больше, чем 100 м:
Так как 1 км = 1 000 м, а 1 000 : 100 = 10.
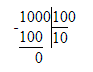
5) Подумаем, во сколько раз 1 м2 больше, чем 1 см2:
Так как 1 м2 = 10 000 см2, значит, м2 больше, чем 1 см2 в 10 000 раз.
Краткое условие: Спортсмен прыгнул на 2 м 35 см, это на 49 см выше его роста. Каков рост спортсмена?

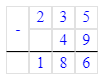
ШАГ 1. Найти рост спортсмена.

1) 2 м 35 см - 49 см = 235 см – 49 см = 186 см = 1 м 86 см – рост спортсмена
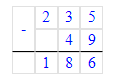
Ответ: рост спортсмена равен 1 м 86 см.
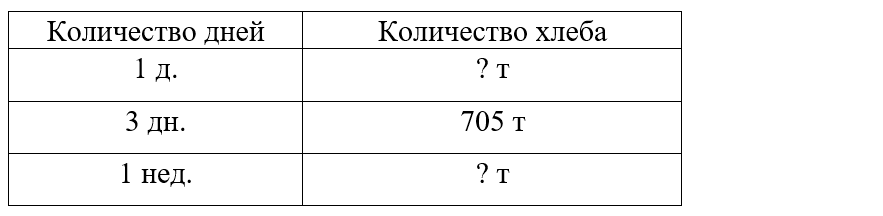
Краткое условие: Хлебозавод ежедневно выпекал одинаковое количество хлеба. За 3 дня выпекли 705 т. Сколько выпекли за неделю?
Неделя - ? т хлеба.
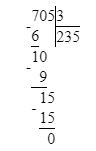
ШАГ 1. Найти сколько хлеба выпекается ежедневно.
ШАГ 2. Найти сколько хлеба выпекается за неделю.
1) 705 : 3 = 235 т – за 1 день
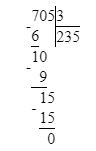
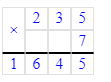
2) 235 · 7 = 1 645 т – за 1 неделю

2) 235 · 7 = 1 645 (т)
Ответ: за 1 неделю выпекается 1 645 т хлеба.
Краткое условие: За 3 ч машина израсходовала 27 л бензина. На сколько часов хватит 96 л, если расход уменьшится на 1 л в час?

2) 9-1=8 (л)- стала расходовать машина в 1 час;
3) 96÷8=на 12 (ч)- езды хватит 96л бензина.
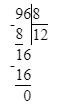
ШАГ 1. Найти расход бензина за час.
ШАГ 2. Найти новый расход.
ШАГ 3. Найти на сколько часов езды хватит 96 л бензина.

1) 27 : 3 = 9 л – начальный расход
Шаг 2. Найдём новый расход:
2) 9 - 1 = 8 л – новый расход
Шаг 3. Найдём на сколько часов езды хватит 96 л бензина:
3) 96 : 8 = 12 ч – время
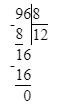
2) 9 - 1 = 8 (л)
3) 96 : 8 = 12 (ч)
Ответ: 96 л бензина хватит на 12 ч езды.
Краткое условие: Вычисли результат и выполни проверку.
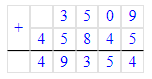
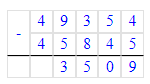
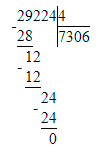
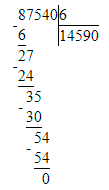
1) 3 509 + 45 845 = 49 354;

49 354 – 45 845 = 3 509;


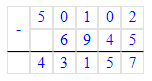
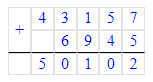
43 157 + 6 945 = 50 102;


29 224 : 4 = 7 306;
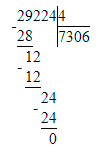
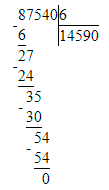
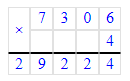
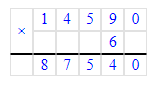
14 590 · 6 = 87 540;

Краткое условие: Реши уравнения.
х=11∙9
х=99
Ответ: х=99.
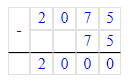
х+75=2 075
х=2 075-75
х=2 000
Ответ: х=2 000.
х∙8=720
х=720÷8
х=90
Ответ: х=90.
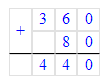
х-80=360
х=360+80
х=440
Ответ: х=440.
56÷х=56
х=56÷56
х=1
Ответ: х=1.
90-х=90
х=90-90
х=0
Ответ: х=0.
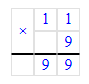
1) х : 9 = 11;
х = 11 · 9;
2) х + 75 = 2 075;
х = 2 075 - 75;
3) х · 8 = 720;
х = 720 : 8;
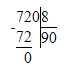
4) х - 80 = 360;
х = 360 + 80;
5) 56 : х = 56;
х = 56 : 56;
х = 1;
6) 90 - х = 90;
х = 90 - 90;
х = 0;
Краткое условие: Найди значение выражения c − k, если c — наименьшее семизначное, k — наибольшее шестизначное число.
k=999 999- наибольшее шестизначное число.
Тогда:
c-k=1 000 000-999 999=1.
1) с = 1 000 000;
2) k = 999 999;
3) с – k = 1 000 000 – 999 999 = 1;
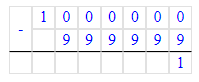
Страница 92. Что узнали. Чему научились. Номер: 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, задача на полях.



