Страница 65, ГДЗ по математике за 4 класс к учебнику Моро часть 1
Страница 65
Краткое условие: Какую часть отрезка АВ составляют отрезки CD (чертеж 1) и МК (чертеж 2)?
На чертеже 2 отрезок AB разделён на 6 равных частей. МК – составляет четыре части, т.е. четыре шестых АВ.
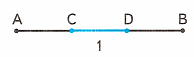
Отрезок АВ разделён на 3 равные части. Отрезок CD составляет 1 часть. Следовательно, отрезок CD составляет одну третью часть отрезка АВ.
3) Рассмотрим чертёж 2:
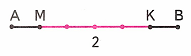
Отрезок АВ разделён на 6 равных частей. Отрезок МК состоит из 4 частей. Следовательно, отрезок МК составляет четыре шестых частей отрезка АВ.
Краткое условие: Начерти отрезок, длина восьмой части которого 8 мм.
Длина отрезка - ? мм.

8 мм · 8 = 64 мм = 6 см 4 мм;
Следовательно, длина отрезка равна 6 см 4 мм.
2) Начертим отрезок АВ найденной длины:
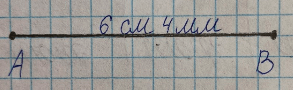
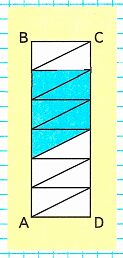
Краткое условие: Найди площадь прямоугольника ABCD в см². 1) На сколько равных треугольников разделён прямоугольник? 2) Найди площадь закрашенной части. 3) Найди площадь незакрашенной части.
1) Прямоугольник ABCD разделён на 12 равных треугольников.
2) Площадь одного такого треугольника равна:
12÷12=1 (см2 ).
Площадь закрашенной части (5 треугольников): 5см2.
3) Площадь незакрашенной части (7 треугольников): 7см2.
1. Длина прямоугольника равна 2 см;
2. Ширина прямоугольника равна 6 см;
3. Площадь прямоугольника равна:
S = a · b = 2 · 6 = 12 см2;
3) Подумаем, на сколько равных треугольников разделён прямоугольник АВСD:
Прямоугольник АВСD разделён на 12 равных треугольников.
4) Найдем площадь закрашенной части прямоугольника:
1. Закрашенная часть прямоугольника состоит из 5 треугольников;
2. Площадь одного треугольника равна:
S = 12 : 12 = 1 см2;
3. Площадь закрашенной части равна:
S = 1 · 5 = 5 см2;
5) Найдем площадь незакрашенной части прямоугольника:
1. Незакрашенная часть прямоугольника состоит из 7 треугольников;
2. Площадь одного треугольника равна:
S = 12 : 12 = 1 см2;
3. Площадь незакрашенной части равна:
S = 1 · 7 = 7 см2;
Краткое условие: Для школы купили 5 мотков провода по 56 м. Израсходовали две седьмых всего провода. Сколько метров осталось?
Израсходовали – две седьмых части;
Осталось -?
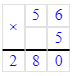
3) 40∙2=80 (м)- провода израсходовали;
4) 280-80=200 (м)- провода осталось.
ШАГ 1. Найти сколько метров провода в 5 мотках.
ШАГ 2. Найти сколько метров провода составляют 1 часть.
ШАГ 3. Найти сколько метров провода израсходовали.
ШАГ 4. Найти сколько метров провода осталось.
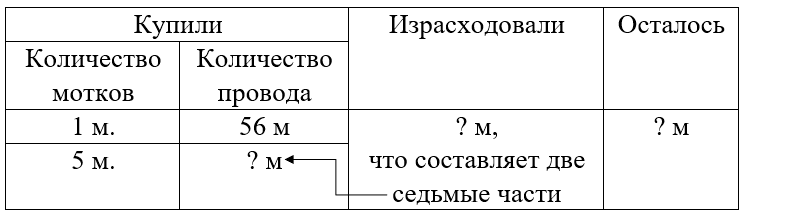
1) 56 · 5 = 280 м – в 5 мотках
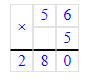
2) 280 : 7 = 40 м – одна часть
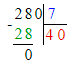
3) 40 · 2 = 80 м – израсходовали
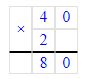
4) 280 - 80 = 200 м – осталось
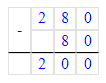
2) 280 : 7 = 40 (м)
3) 40 · 2 = 80 (м)
4) 280 - 80 = 200 (м)
Ответ: осталось 200 м провода.
Краткое условие: За 3 ч бульдозер разровнял 234 м² дороги. Сколько м² он разровняет за 10 ч при той же производительности?
За 10 часов - ? м2 дороги.
2) 78∙10=780 (м2 )-дороги разровняет бульдозер за 10 часов.
ШАГ 1. Найти сколько производительность бульдозера.
ШАГ 2. Найти сколько квадратных метров дороги разровняет бульдозер за 10 ч.
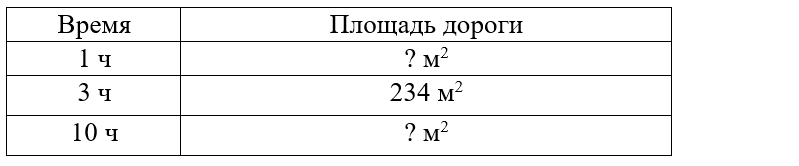
1) 234 : 3 = 78 м2 – за 1 час
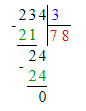
2) 78 · 10 = 780 м2 – за 10 часов
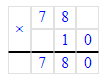
2) 78 · 10 = 780 (м2)
Ответ: за 10 часов бульдозер разровняет 780 м2 дороги.
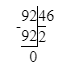
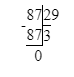
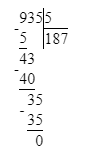
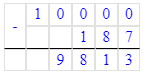
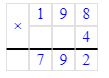
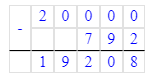

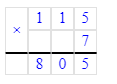
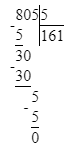
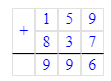
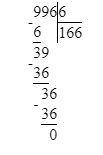
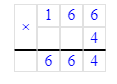
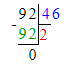
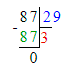
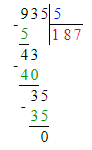





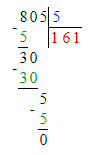

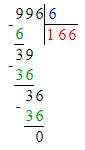

Краткое условие: Проверь, правильно ли выполнено деление с остатком.
Проверяем:
1) 6<8- верно
2) 8∙9=72
3) 72+6=78- неверно.
Должно быть так : 78÷8=9 (ост.6).
793÷6=132 (ост.1);
Проверяем:
1) 1<6- верно
2) 132∙6=792
3)792+1=793- верно.
54÷11=4(ост.10);
Проверяем:
1) 10<11- верно
2) 11∙4=44
3) 44+10=54-верно.
612÷7=87 (ост.4)
Проверяем:
1) 4<7- верно
2) 87∙7=609
3) 609+4=613- неверно.
Должно быть так: 613÷7=87 (ост.4).
1) 76 : 8 = 9 (ост. 4);
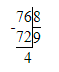
Следовательно, деление с остатком в начальном условии решено неверно.
2) 793 : 6 = 132 (ост. 1);
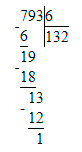
Следовательно, деление с остатком в начальном условии решено верно.
3) 54 : 11 = 4 (ост. 10);
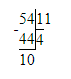
Следовательно, деление с остатком в начальном условии решено верно.
4) 612 : 7 = 87 (ост. 3);
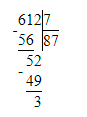
Следовательно, деление с остатком в начальном условии решено неверно.
Краткое условие: Лимоны раскладывали в корзины по 100 штук. Заполнили 15 корзин, осталось 30 лимонов.

2) 1 500+30= 1 530 (лимонов) - было всего.
ШАГ 1. Найти количество лимонов в 15 корзинах.
ШАГ 2. Найти общее количество лимонов.

1) 100 · 15 = 1 500 л. – в 15 корзинах
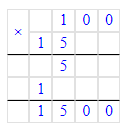
2) 1 500 + 30 = 1 530 л. – всего
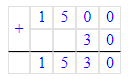
2) 1 500 + 30 = 1 530 (л.)
Ответ: было 1 530 лимонов.
Краткое условие: Сравни значения величин.
400 м<1 км, так как в 1 км=1 000 м;
5 м2>50дм2, так как 5 м2 = 500 дм2;
400 000 м2<1 км2, так как 1 км2 = 1 000 000 м2.
1) 5 м и 50 дм;
Так как 1 м = 10 дм, то 5 м = 50 дм, следовательно, 5 м = 50 дм.
2) 400 м и 1 км;
Так как 1 км = 1 000 м, то 400 м < 1 000 м, следовательно, 400 м < 1 км
3) 5 м2 и 50 дм2;
Так как 1 м2 = 100 дм2, то 5 м2 = 500 дм2, а 500 дм2 > 50 дм2. Следовательно, 5 м2 > 50 дм2;
4) 400 000 м2 и 1 км2;
Так как 1 км2 = 1 000 000 м2, то 400 000 м2 < 1 км2;
Краткое условие: Таня нашла на 15 орехов больше Марины и отдала ей 8 орехов. У кого и на сколько стало больше орехов?
2) 8-7=на 1 (орех) - больше стало у Марины.
ШАГ 1. Найти сколько орехов из 15 разницы осталось.
ШАГ 2. Найти у кого из девочек стало больше орехов и на сколько.
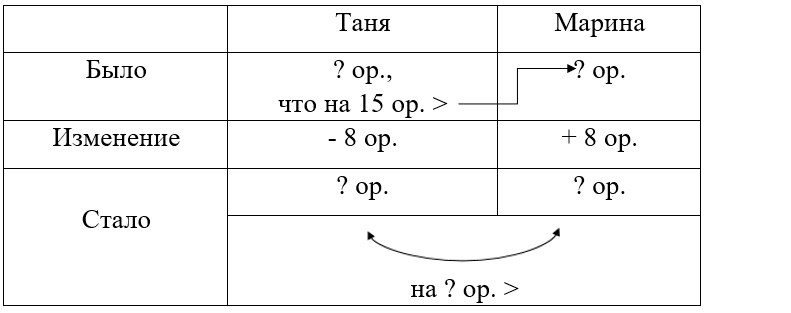
1) 15 – 8 = 7 ор. – осталось из разницы
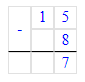
2) 8 - 7 = 1 ор. – на столько больше орехов у Марины
2) 8 - 7 = 1 (ор.)
Ответ: у Марины стало на 1 орех больше.
Краткое условие: Начерти отрезок, длина третьей части которого 20 мм.
20 мм · 3 = 60 мм = 6 см;
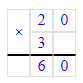
2) Начертим отрезок АВ найденной длины:
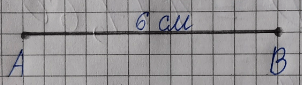
Страница 65. Номер: 300, 301, 302, 303, 304, 305, 306, 307, 308, 309, задача на полях.



