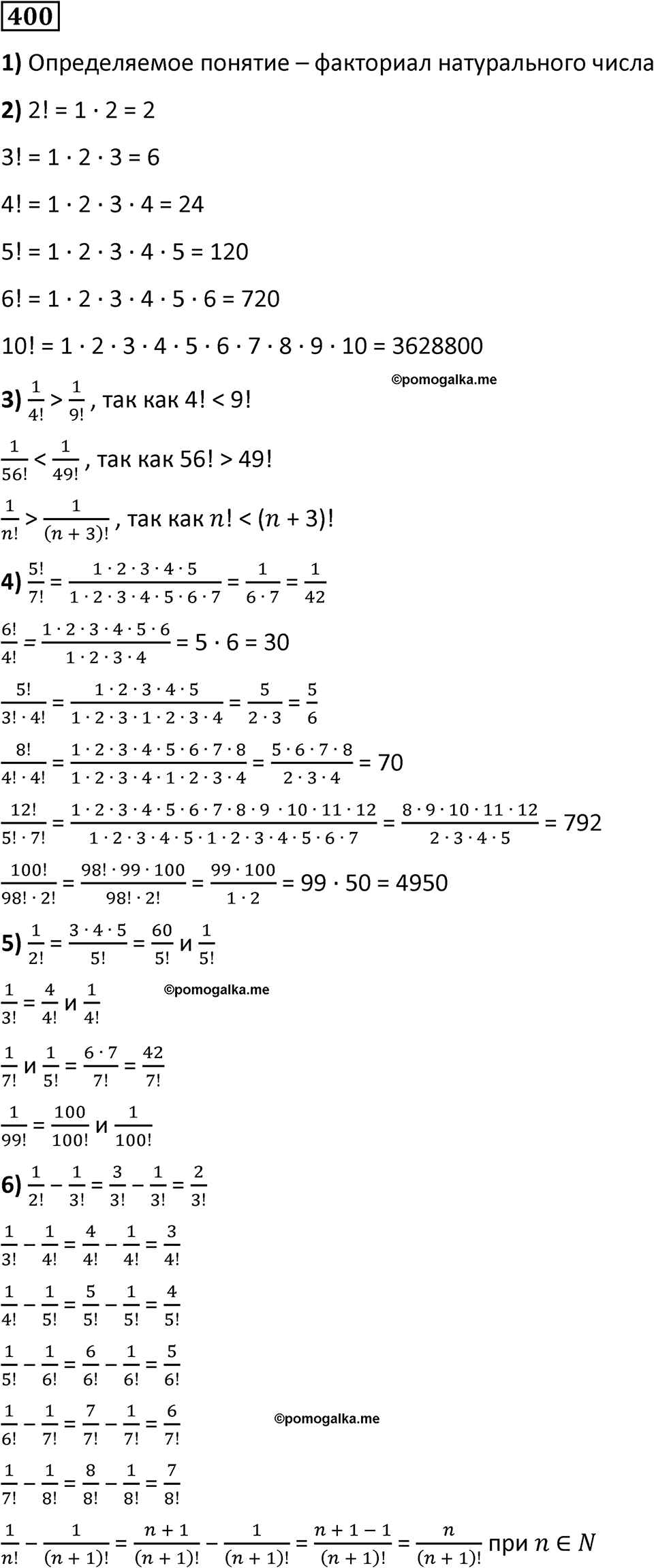Часть 2 страница 81 номер 400, ГДЗ по математике за 5 класс к учебнику Дорофеева, Петерсона

Краткое условие: 1) Назови понятие. 2) Вычисли: 2!, 3!, 4!, 5!, 6!, 10!. 3) Сравни: \( \frac{1}{4!} \) и \( \frac{1}{9!}, \frac{1}{56!} \) и \( \frac{1}{49!}, \frac{1}{n!} \) и \( \frac{1}{(n+3)!} \). 4) Приведи к несократимому виду: \(\frac{5!}{7!}, \frac{6!}{4!}, \frac{5!}{3!\cdot 4!}, \frac{8!}{4!\cdot 4!}, \frac{12!}{5!\cdot 7!}, \frac{100!}{98!\cdot 2!}\). 5) Приведи к общему знаменателю: \(\frac{1}{2!}\) и \(\frac{1}{5!}, \frac{1}{3!}\) и \(\frac{1}{4!}, \frac{1}{7!}\) и \(\frac{1}{5!}, \frac{1}{99!}\) и \(\frac{1}{100!}\). 6) Найди разности: \(\frac{1}{2!}-\frac{1}{3!}, \frac{1}{3!}-\frac{1}{4!}, \frac{1}{4!}-\frac{1}{5!}, \frac{1}{5!}-\frac{1}{6!}\). Запиши две разности и найди их значение. Чему равна разность \(\frac{1}{n!}-\frac{1}{(n+1)!}\)?