4класс
Страница 91, ГДЗ по математике за 4 класс к учебнику Моро часть 1
Страница 91
Номер задания: 1
Краткое условие: Объясни, почему верны равенства.
Решение:
1)
Данное равенство верно по распределительному свойству относительно сложения.
170∙3+170=170∙4
170∙3+170∙1=170∙4
170∙(3+1)=170∙4
170∙4=170∙4 – верно.
Данное равенство верно по распределительному свойству относительно вычитания.
560∙9-560=560∙8
560∙9-560∙1=560∙8
560∙(9-1)=560∙8
560∙8=560∙8- верно.
Данное равенство верно по распределительному свойству относительно сложения.
96∙4+96∙6=96∙10
96∙(4+6)=96∙10
96∙10=96∙10- верно.
Данное равенство верно по переместительному свойству сложения(умножения).
45∙3+450=450+3∙45- верно.
2)
Данное равенство верно по правилу деления суммы на число.
(81+27)÷9=81÷9+27÷9- верно.
Данное равенство верно по правилу деления разности на число.
(540-180)÷6=540÷6-180÷6- верно.
Данное равенство верно по распределительному свойству относительно сложения.
170∙3+170=170∙4
170∙3+170∙1=170∙4
170∙(3+1)=170∙4
170∙4=170∙4 – верно.
Данное равенство верно по распределительному свойству относительно вычитания.
560∙9-560=560∙8
560∙9-560∙1=560∙8
560∙(9-1)=560∙8
560∙8=560∙8- верно.
Данное равенство верно по распределительному свойству относительно сложения.
96∙4+96∙6=96∙10
96∙(4+6)=96∙10
96∙10=96∙10- верно.
Данное равенство верно по переместительному свойству сложения(умножения).
45∙3+450=450+3∙45- верно.
2)
Данное равенство верно по правилу деления суммы на число.
(81+27)÷9=81÷9+27÷9- верно.
Данное равенство верно по правилу деления разности на число.
(540-180)÷6=540÷6-180÷6- верно.
Решение:
Объясним, почему верны равенства:
1)
1. 170 · 3 + 170 = 170 · 4;
Данное выражение верно, так как применяется распределительный закон умножения относительно сложения:
170 · 3 + 170 = 170 · (3 + 1) = 170 · 4;
2. 560 · 9 - 170 = 560 · 8;
Данное выражение верно, так как применяется распределительный закон умножения относительно вычитания:
560 · 9 - 170 = 560 · (9 - 1) = 560 · 8;
3. 96 · 4 + 96 · 6 = 96 · 10;
Данное выражение верно, так как применяется распределительный закон умножения относительно сложения:
96 · 4 + 96 · 6 = 96 · (4 + 6) = 96 · 10;
4. 45 · 3 + 450 = 450 + 3 · 45;
Данное выражение верно, так как применяется переместительный закон сложения, а также переместительный закон умножения;
2)
1. (81 + 27) : 9 = 81 : 9 + 27 : 9;
Данное выражение верно, так как применяется правило деления суммы чисел на число;
2. (540 - 180) : 6 = 540 : 6 - 180 : 6;
Данное выражение верно, так как применяется правило деления разности чисел на число;
1)
1. 170 · 3 + 170 = 170 · 4;
Данное выражение верно, так как применяется распределительный закон умножения относительно сложения:
170 · 3 + 170 = 170 · (3 + 1) = 170 · 4;
2. 560 · 9 - 170 = 560 · 8;
Данное выражение верно, так как применяется распределительный закон умножения относительно вычитания:
560 · 9 - 170 = 560 · (9 - 1) = 560 · 8;
3. 96 · 4 + 96 · 6 = 96 · 10;
Данное выражение верно, так как применяется распределительный закон умножения относительно сложения:
96 · 4 + 96 · 6 = 96 · (4 + 6) = 96 · 10;
4. 45 · 3 + 450 = 450 + 3 · 45;
Данное выражение верно, так как применяется переместительный закон сложения, а также переместительный закон умножения;
2)
1. (81 + 27) : 9 = 81 : 9 + 27 : 9;
Данное выражение верно, так как применяется правило деления суммы чисел на число;
2. (540 - 180) : 6 = 540 : 6 - 180 : 6;
Данное выражение верно, так как применяется правило деления разности чисел на число;
Номер задания: 2
Решение:
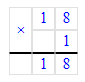
1∙43+54∙0=43+0=43;
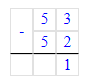
81∙1-0∙32=81-0=81;
81∙1-0∙32=81-0=81;
(84 - 7 ∙ 12) ∙ 35=0;
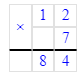

84-84=0;
0∙35=0.
75 ∙ (48 - 2 ∙ 24)=0;
2∙24=48;
48-48=0;
75∙0=0.
(90 - 89) ∙ 35=35;
90-89=1;
1∙35=35.
18 ∙ (53 - 52)=18.
53-52=1;
18∙1=18.
Решение:
1) 1 · 43 + 54 ∙ 0 = 43;
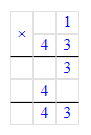
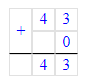

54 · 0 = 0

2) 81 · 1 - 0 ∙ 32 = 81;
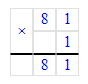
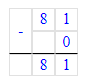

0 · 32 = 0

3) (84 - 7 ∙ 12) ∙ 35=0;


84-84=0;
0∙35=0.
4) 75 ∙ (48 - 2 ∙ 24)=0;
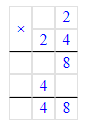

48-48=0;
75∙0=0.
5) (90 - 89) ∙ 35=35;
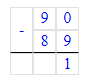
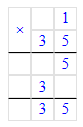


6) 18 ∙ (53 - 52)=18.


Ответ:
1) 43; 2) 81; 3) 0; 4) 0; 5) 35; 6) 18.
Номер задания: 3
Решение:
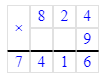
824∙9=7 416;
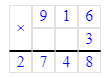
 916∙3=2 748;
916∙3=2 748;
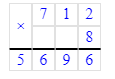
 712∙8=5 696;
712∙8=5 696;
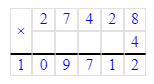
 27 428∙4=109 712;
27 428∙4=109 712;
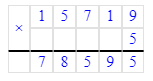
 15 719∙5=78 595;
15 719∙5=78 595;
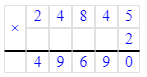
 2∙24 845=24 845∙2=49 690;
2∙24 845=24 845∙2=49 690;
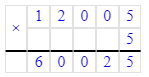
 12 005∙5=60 025;
12 005∙5=60 025;
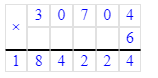
 30 704∙6=184 224;
30 704∙6=184 224;
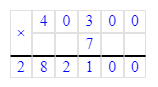
 7∙40 300=40 300∙7=282 100;
7∙40 300=40 300∙7=282 100;
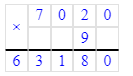
 7 020∙9=63 180;
7 020∙9=63 180;
 7 002∙9=63 018;
7 002∙9=63 018;
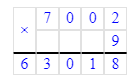 7 200∙9=64 800.
7 200∙9=64 800.












Решение:
1) 824∙9=7 416;
 2) 916∙3=2 748;
2) 916∙3=2 748;
 3) 712∙8=5 696;
3) 712∙8=5 696;
 4) 27 428∙4=109 712;
4) 27 428∙4=109 712;
 5) 15 719∙5=78 595;
5) 15 719∙5=78 595;
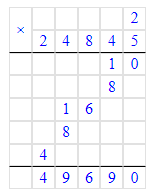
 6) 2∙24 845=24 845∙2=49 690;
6) 2∙24 845=24 845∙2=49 690;
 7) 12 005∙5=60 025;
7) 12 005∙5=60 025;
 8) 30 704∙6=184 224;
8) 30 704∙6=184 224;
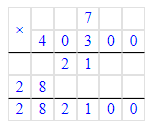
 9) 7∙40 300=40 300∙7=282 100;
9) 7∙40 300=40 300∙7=282 100;
 10) 7 020∙9=63 180;
10) 7 020∙9=63 180;
 11) 7 002∙9=63 018;
11) 7 002∙9=63 018;
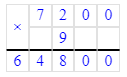
 12) 7 200∙9=64 800.
12) 7 200∙9=64 800.













Ответ:
1) 7 416; 2) 2 748; 3) 5 696; 4) 109 712; 5) 78 595; 6) 49 690; 7) 60 025; 8) 184 224; 9) 282 100; 10) 63 180; 1) 63 018; 12) 64 800.
Номер задания: 4
Решение:
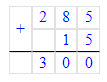
(285 + 15) : 3 ∙ 5 + 280=780;
285+15=300;
300÷3=100;
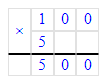
100∙5=500;
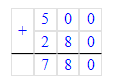
500+280=780.
400 - (60 + 30) : 10 ∙ 1=391;
60+30=90;
90÷10=9;
9∙1=9;
400-9=391.
(300 - 100) - 100 : (10 : 5)=150;
300-100=200;
10÷5=2;
100÷2=50;
200-50=150.
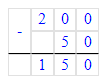
300 - (100 - 100) : (10 : 5)=300.
100-100=0;
10÷5=2;
0÷2=0;
300-0=300.
Решение:
1) (285 + 15) : 3 ∙ 5 + 280=780;
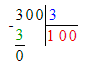

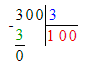


2) 400 - (60 + 30) : 10 ∙ 1=391;
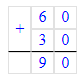
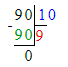

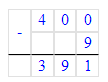

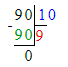


3) (300 - 100) - 100 : (10 : 5)=150;
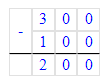
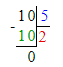
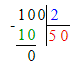

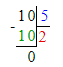
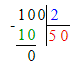

4) 300 - (100 - 100) : (10 : 5)=300.
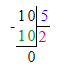
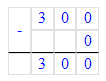
100 – 100 = 0
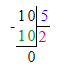
0÷2=0;

Ответ:
1) 780; 2) 391; 3) 150; 4) 300.
Номер задания: 5
Решение:
657∙4=2 628;
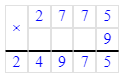
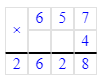 509∙7=3 563;
509∙7=3 563;
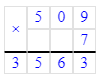 2 193∙5=10 965;
2 193∙5=10 965;
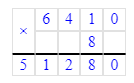
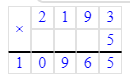 7 640∙8=61 120;
7 640∙8=61 120;
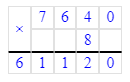 40 018∙9=360 162;
40 018∙9=360 162;
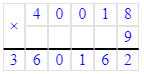 80 700∙6=484 200;
80 700∙6=484 200;
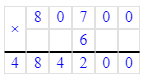






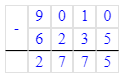
(9 010 - 6 235) ∙ 9=24 975;


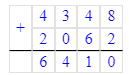
8 ∙ (4 348 + 2 062)=51 280.


Решение:
1) 657∙4=2 628;
 2) 509∙7=3 563;
2) 509∙7=3 563;
 3) 2 193∙5=10 965;
3) 2 193∙5=10 965;
 4) 7 640∙8=61 120;
4) 7 640∙8=61 120;
 5) 40 018∙9=360 162;
5) 40 018∙9=360 162;
 6) 80 700∙6=484 200;
6) 80 700∙6=484 200;







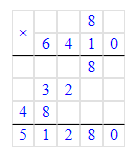
7) (9 010 - 6 235) ∙ 9=24 975;




8) 8 ∙ (4 348 + 2 062)=51 280.



Ответ:
1) 2 628; 2) 3 563; 3) 10 965; 4) 61 120; 5) 360 162; 6) 484 200; 7) 24 975; 8) 51 280.
Номер задания: 6
Краткое условие: Увеличь в 8 раз числа: 700, 900, 1200. Уменьши в 7 раз числа: 560, 98, 1400.
Решение:
Увеличим в 8 раз каждое из чисел: 700, 900, 1200.
700∙8=5 600;
900∙8=7 200;
1 200∙8=9 600.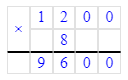 Уменьшим в 7 раз каждое из чисел: 560; 98; 1400.
Уменьшим в 7 раз каждое из чисел: 560; 98; 1400.
560÷7=80;
98÷7=14;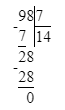 1 400÷7=200.
1 400÷7=200.
700∙8=5 600;
900∙8=7 200;
1 200∙8=9 600.

560÷7=80;
98÷7=14;
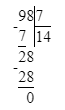
Решение:
1) Увеличим в 8 раз каждое из чисел:
1. 700 · 8 = 5 600;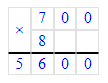 2. 900 · 8 = 7 200;
2. 900 · 8 = 7 200;
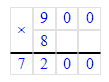 3. 1 200 · 8 = 9 600;
3. 1 200 · 8 = 9 600;
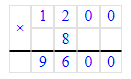 2) Уменьшим в 7 раз каждое из чисел:
2) Уменьшим в 7 раз каждое из чисел:
1. 560 : 7 = 80;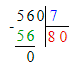 2. 98 : 7 = 14;
2. 98 : 7 = 14;
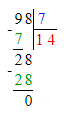 3. 1 400 : 7 = 200;
3. 1 400 : 7 = 200;
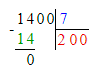
1. 700 · 8 = 5 600;



1. 560 : 7 = 80;
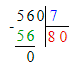
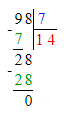
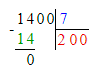
Ответ:
1) 5 600; 7 200; 9 600; 2) 80; 14; 200.
Номер задания: 7
Краткое условие: Сначала объясни, в каком уравнении каждой пары х больше, затем проверь вычислением.
Решение:
В уравнениях 1 пары необходимо найти вычитаемое. Чтобы найти вычитаемое надо из уменьшаемого вычесть разность. При одинаковых уменьшаемых, вычитаемое больше там, где меньше разность. Значение х больше в первом уравнении.
400-х=170
х=400-170
х=230.
400-х=270
х=400-270
х=130.
В уравнениях 2 пары необходимо найти уменьшаемое. Чтобы найти уменьшаемое надо к разности прибавить вычитаемое. При одинаковых вычитаемых, уменьшаемое больше там, где больше разность. Значение х больше в первом уравнении.
х-80=90∙7
х-80=630
х=630+80
х=710.
х-80=90∙5
х-80=450
х=450+80
х=530.
В уравнениях 3 пары необходимо найти делимое. Чтобы найти делимое надо частное умножить на делитель. При одинаковых делителях, делимое больше там, где больше частное. Значение х больше во втором уравнении.
х÷6=56+44
х÷6=100
х=100∙6
х=600.
х÷6=156+44
х÷6=200
х=200∙6
х=1 200.
400-х=170
х=400-170
х=230.
400-х=270
х=400-270
х=130.
В уравнениях 2 пары необходимо найти уменьшаемое. Чтобы найти уменьшаемое надо к разности прибавить вычитаемое. При одинаковых вычитаемых, уменьшаемое больше там, где больше разность. Значение х больше в первом уравнении.
х-80=90∙7
х-80=630
х=630+80
х=710.
х-80=90∙5
х-80=450
х=450+80
х=530.
В уравнениях 3 пары необходимо найти делимое. Чтобы найти делимое надо частное умножить на делитель. При одинаковых делителях, делимое больше там, где больше частное. Значение х больше во втором уравнении.
х÷6=56+44
х÷6=100
х=100∙6
х=600.
х÷6=156+44
х÷6=200
х=200∙6
х=1 200.
Решение:
Сначала объясним, в каком из уравнений каждой пары значение х будет больше, а потом проверим вычислением:
1) В первой паре больше неизвестное число в первом уравнении, так как при его решении от уменьшаемого будет вычитаться меньшее число. Значит, разность будет больше.
1. 400 - х = 170;
х = 400 – 170;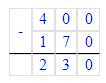 х = 230;
х = 230;
2. 400 - х = 270;
х = 400 – 270;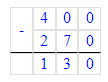 х = 130;
х = 130;
Так как 230 > 130, то неизвестное первого уравнения больше.
2) Во второй паре больше неизвестное число в первом уравнении, так как при его решении к вычитаемому будет прибавляться большее число. Значит, уменьшаемое будет больше.
1. х - 80 = 90 · 7;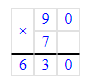 х - 80 = 630;
х - 80 = 630;
х = 630 + 80;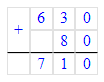 х = 710;
х = 710;
2. х - 80 = 90 · 5;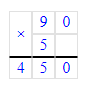 х - 80 = 450;
х - 80 = 450;
х = 450 + 80;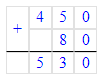 х = 530;
х = 530;
Так как 710 > 530, то неизвестное первого уравнения больше.
3) В третьей паре больше неизвестное число во втором уравнении, так как при его решении делитель будет умножаться на большее число. Значит, делитель будет больше.
1. х : 6 = 56 + 44;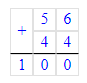 х : 6 = 100;
х : 6 = 100;
х = 100 · 6;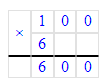 х = 600;
х = 600;
2. х : 6 = 156 + 44;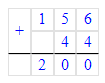 х : 6 = 200;
х : 6 = 200;
х = 200 · 6;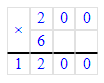 х = 1 200;
х = 1 200;
Так как 1 200 > 600, то неизвестное второго уравнения больше.
1) В первой паре больше неизвестное число в первом уравнении, так как при его решении от уменьшаемого будет вычитаться меньшее число. Значит, разность будет больше.
1. 400 - х = 170;
х = 400 – 170;

2. 400 - х = 270;
х = 400 – 270;

Так как 230 > 130, то неизвестное первого уравнения больше.
2) Во второй паре больше неизвестное число в первом уравнении, так как при его решении к вычитаемому будет прибавляться большее число. Значит, уменьшаемое будет больше.
1. х - 80 = 90 · 7;

х = 630 + 80;

2. х - 80 = 90 · 5;

х = 450 + 80;

Так как 710 > 530, то неизвестное первого уравнения больше.
3) В третьей паре больше неизвестное число во втором уравнении, так как при его решении делитель будет умножаться на большее число. Значит, делитель будет больше.
1. х : 6 = 56 + 44;

х = 100 · 6;

2. х : 6 = 156 + 44;

х = 200 · 6;

Так как 1 200 > 600, то неизвестное второго уравнения больше.
Ответ:
1) х = 230; х = 130; 2) х = 710; х = 530; 3) х = 600; х = 1 200.
Номер задания: 8
Краткое условие: Выполни деление с остатком и проверь.
Решение:
20÷3=6 (ост.2).
Проверка: 6∙3+2=20.
35÷8=3 (ост.11).
Проверка: 3∙8+11=35.
244÷7=34 (ост.6).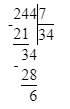 Проверка: 34∙7+6=244.
Проверка: 34∙7+6=244.
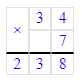
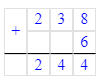
6 539÷5=1 307 (ост.4).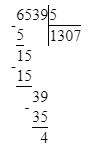 Проверка: 1 307∙5+4=6 539.
Проверка: 1 307∙5+4=6 539.
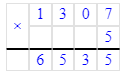
8 969÷9=996 (ост.5).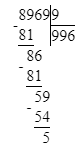 Проверка: 996∙9+5=8 969.
Проверка: 996∙9+5=8 969.
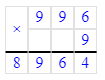
5 219÷9=579 (ост.8).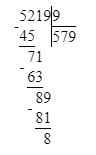 Проверка: 579∙9+8=5 219.
Проверка: 579∙9+8=5 219.
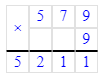
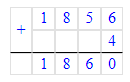
1 860÷8=232 (ост.4).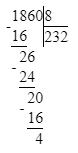 Проверка: 232∙8+4=1 860.
Проверка: 232∙8+4=1 860.
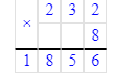
217÷400=0 (ост.217).
Проверка: 0∙400+217=217.
130÷400=0 (ост.130).
Проверка: 0∙400+130=130.
Проверка: 6∙3+2=20.
35÷8=3 (ост.11).
Проверка: 3∙8+11=35.
244÷7=34 (ост.6).
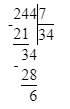


6 539÷5=1 307 (ост.4).
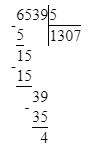

8 969÷9=996 (ост.5).
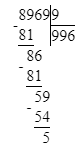

5 219÷9=579 (ост.8).
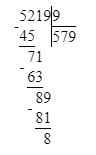

1 860÷8=232 (ост.4).
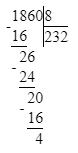

217÷400=0 (ост.217).
Проверка: 0∙400+217=217.
130÷400=0 (ост.130).
Проверка: 0∙400+130=130.
Решение:
Выполним деление с остатком и проверим:
1) 20 : 3 = 6 (ост. 2)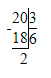 Проверка:
Проверка:
1) 2 < 3;
2) 3 · 6 = 18;
3) 18 + 2 = 20;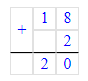 2) 35 : 8 = 4 (ост. 3)
2) 35 : 8 = 4 (ост. 3)
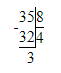 Проверка:
Проверка:
1) 3 < 8;
2) 4 · 8 = 32;
3) 32 + 3 = 35;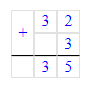 3) 244 : 7 = 34 (ост. 6)
3) 244 : 7 = 34 (ост. 6)
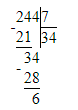 Проверка:
Проверка:
1) 6 < 7;
2) 34 · 7 = 238;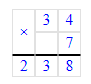 3) 238 + 6 = 244;
3) 238 + 6 = 244;
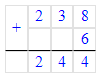 4) 167 : 9 = 18 (ост. 5)
4) 167 : 9 = 18 (ост. 5)
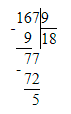 Проверка:
Проверка:
1) 5 < 9;
2) 18 · 9 = 162;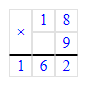 3) 162 + 5 = 167;
3) 162 + 5 = 167;
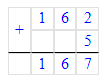 5) 6 539 : 5 = 1 307 (ост. 4)
5) 6 539 : 5 = 1 307 (ост. 4)
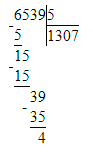 Проверка:
Проверка:
1) 4 < 5;
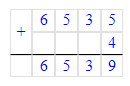
2) 1 307 · 5 = 6 535;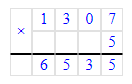 3) 6 535 + 4 = 6 539;
3) 6 535 + 4 = 6 539;
 6) 8 969 : 9 = 996 (ост. 5)
6) 8 969 : 9 = 996 (ост. 5)
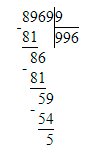 Проверка:
Проверка:
1) 5 < 9;
2) 996 · 9 = 8 964;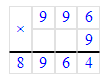 3) 8 964 + 5 = 8 969;
3) 8 964 + 5 = 8 969;
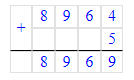 7) 5 219 : 9 = 579 (ост. 8)
7) 5 219 : 9 = 579 (ост. 8)
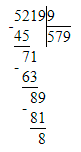 Проверка:
Проверка:
1) 8 < 9;
2) 579 · 9 = 5 211;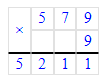 3) 5 211 + 8 = 5 219;
3) 5 211 + 8 = 5 219;
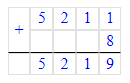 8) 1 860 : 8 = 232 (ост. 4)
8) 1 860 : 8 = 232 (ост. 4)
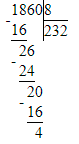 Проверка:
Проверка:
1) 4 < 8;
2) 232 · 8 = 1 856;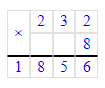 3) 1 856 + 4 = 1 860;
3) 1 856 + 4 = 1 860;
 9) 217 : 400 = 0 (ост. 217)
9) 217 : 400 = 0 (ост. 217)
Проверка:
1) 217 < 400;
2) 0 · 400 = 0;
3) 0 + 217 = 217;
10) 130 : 400 = 0 (ост. 130)
Проверка:
1) 130 < 400;
2) 0 · 400 = 0;
3) 0 + 130 = 130;
1) 20 : 3 = 6 (ост. 2)
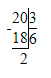
1) 2 < 3;
2) 3 · 6 = 18;
3) 18 + 2 = 20;

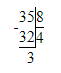
1) 3 < 8;
2) 4 · 8 = 32;
3) 32 + 3 = 35;

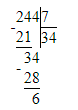
1) 6 < 7;
2) 34 · 7 = 238;


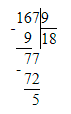
1) 5 < 9;
2) 18 · 9 = 162;


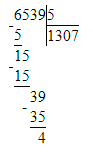
1) 4 < 5;
2) 1 307 · 5 = 6 535;


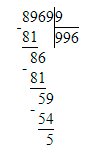
1) 5 < 9;
2) 996 · 9 = 8 964;


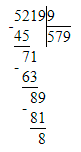
1) 8 < 9;
2) 579 · 9 = 5 211;


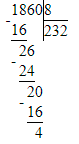
1) 4 < 8;
2) 232 · 8 = 1 856;


Проверка:
1) 217 < 400;
2) 0 · 400 = 0;
3) 0 + 217 = 217;
10) 130 : 400 = 0 (ост. 130)
Проверка:
1) 130 < 400;
2) 0 · 400 = 0;
3) 0 + 130 = 130;
Ответ:
1) 6 (ост. 2); 2) 4 (ост. 3); 3) 34 (ост. 6); 4) 18 (ост. 5); 5) 1 307 (ост. 4); 6) 996 (ост. 5); 7) 579 (ост. 8); 8) 232 (ост. 4); 9) 0 (ост. 217); 10) 0 (ост. 130).
Номер задания: 9
Краткое условие: Вычисли и сделай проверку.
Решение:
7 410÷3=2470;
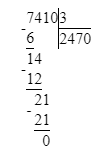 Проверка:
Проверка:
 4 850÷5=970;
4 850÷5=970;
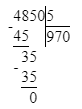 Проверка:
Проверка:
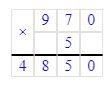 618÷6=103;
618÷6=103;
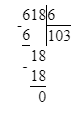 Проверка:
Проверка:
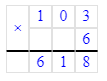 912÷3=304;
912÷3=304;
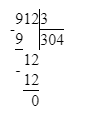 Проверка:
Проверка:
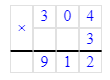 37 600÷4=9 400;
37 600÷4=9 400;
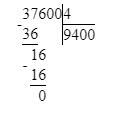 Проверка:
Проверка:
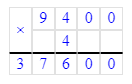 81 600÷6=13 600;
81 600÷6=13 600;
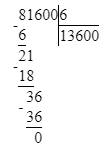 Проверка:
Проверка:
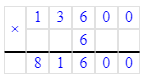 424 000÷4=106 000;
424 000÷4=106 000;
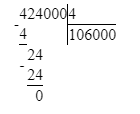 Проверка:
Проверка:
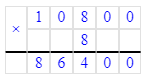
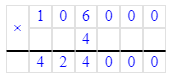 86 400÷8=10 800;
86 400÷8=10 800;
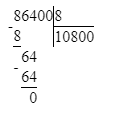 Проверка:
Проверка:
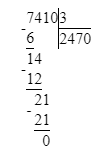

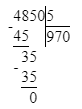

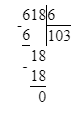

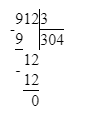

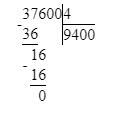

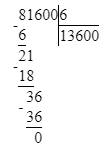

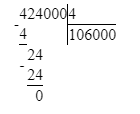

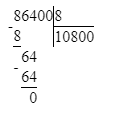

Решение:
Вычислим и сделаем проверку:
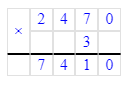
1) 7 410 : 3 = 2 470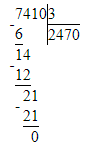 Проверка:
Проверка:
2 470 · 3 = 7 410;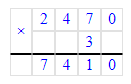 7 410 = 7 410;
7 410 = 7 410;
2) 4 850 : 5 = 970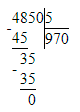 Проверка:
Проверка:
970 · 5 = 4 850;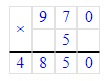 4 850 = 4 850;
4 850 = 4 850;
3) 618 : 6 = 103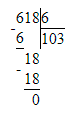 Проверка:
Проверка:
103 · 6 = 618;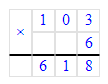 618 = 618;
618 = 618;
4) 912 : 3 = 304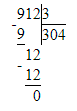 Проверка:
Проверка:
304 · 3 = 912;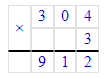 912 = 912;
912 = 912;
5) 37 600 : 4 = 9 400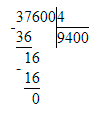 Проверка:
Проверка:
9 400 · 4 = 37 600;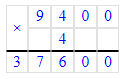 37 600 = 37 600;
37 600 = 37 600;
6) 81 600 : 6 = 13 600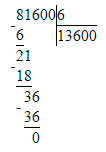 Проверка:
Проверка:
13 600 · 6 = 81 600;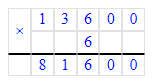 81 600 = 81 600;
81 600 = 81 600;
7) 424 000 : 4 = 106 000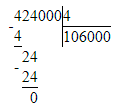 Проверка:
Проверка:
106 000 · 4 = 424 000;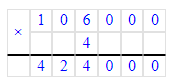 424 000 = 424 000;
424 000 = 424 000;
8) 86 400 : 8 = 10 800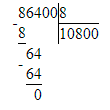 Проверка:
Проверка:
10 800 · 8 = 86 400;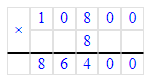 86 400 = 86 400;
86 400 = 86 400;
1) 7 410 : 3 = 2 470
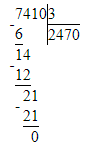
2 470 · 3 = 7 410;

2) 4 850 : 5 = 970
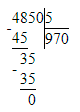
970 · 5 = 4 850;

3) 618 : 6 = 103
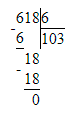
103 · 6 = 618;

4) 912 : 3 = 304
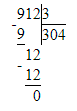
304 · 3 = 912;

5) 37 600 : 4 = 9 400
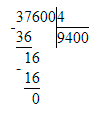
9 400 · 4 = 37 600;

6) 81 600 : 6 = 13 600
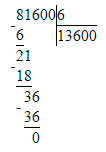
13 600 · 6 = 81 600;

7) 424 000 : 4 = 106 000
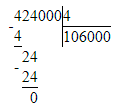
106 000 · 4 = 424 000;

8) 86 400 : 8 = 10 800
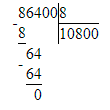
10 800 · 8 = 86 400;

Ответ:
1) 2 470; 2) 970; 3) 103; 4) 304; 5) 9 400; 6) 13 600; 7) 106 000; 8) 10 800.
Номер задания: 10
Решение:
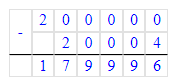
200 000 - 160 032 : 8=179 996;
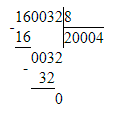
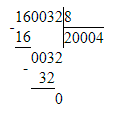

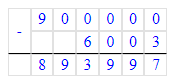
900 000 - 54 027 : 9=893 997;
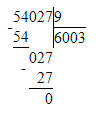
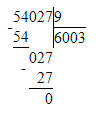

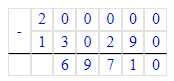
200 000 - 521 160 : 4=69 710;
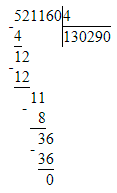
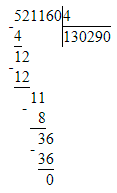

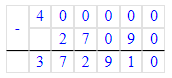
400 000 - 81 270 : 3=372 910.
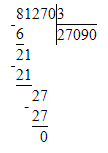
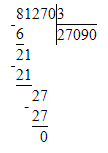

Решение:
1) 200 000 - 160 032 : 8=179 996;
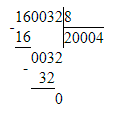

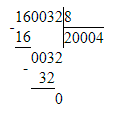

2) 900 000 - 54 027 : 9=893 997;
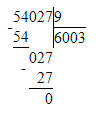

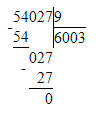

3) 200 000 - 521 160 : 4=69 710;
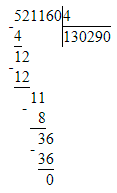

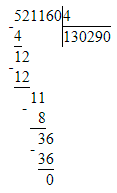

4) 400 000 - 81 270 : 3=372 910.
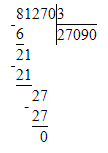

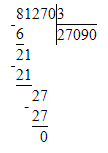

Ответ:
1) 179 996; 2) 893 997; 3) 69 710; 4) 372 910.
Номер задания: 11
Краткое условие: Объясни, почему неравенства верны.
Решение:
Применим распределительное свойство умножения: вынесем общий множитель за скобки.
170∙5+8∙5>169∙5+6∙5
5∙(170+8)>5∙(169+6)
5∙178>5∙175- неравенство верно потому что множитель слева больше, чем справа (178>175).
Найдём значения выражений в скобках:
6 102∙(81÷81)>6 102∙(81-81)
6 102∙1>6 102∙0- неравенство верно потому что множитель слева больше, чем справа (1>0).
При одинаковом делимом частное больше там, где меньше делитель.
676÷4<676÷2-неравенство верно.
Произведение больше там, где больше множители:
359∙4>359∙3-неравенство верно.
170∙5+8∙5>169∙5+6∙5
5∙(170+8)>5∙(169+6)
5∙178>5∙175- неравенство верно потому что множитель слева больше, чем справа (178>175).
Найдём значения выражений в скобках:
6 102∙(81÷81)>6 102∙(81-81)
6 102∙1>6 102∙0- неравенство верно потому что множитель слева больше, чем справа (1>0).
При одинаковом делимом частное больше там, где меньше делитель.
676÷4<676÷2-неравенство верно.
Произведение больше там, где больше множители:
359∙4>359∙3-неравенство верно.
Решение:
Объясним, почему неравенства верны:
1) 170 · 5 + 8 · 5 > 169 · 5 + 6 · 5;
Данное неравенство верно, так как больше то произведение, где больше множители.
2) 6 102 · (81 : 81) > 6 102 · (81 – 81);
Частное чисел 81 и 81 равняется 1, а разность чисел 81 и 81 равняется 0. Соответственно, выражение слева больше.
3) 676 : 4 < 676 : 2;
Данное неравенство верно, так как больше то частное, где меньше делитель.
4) 359 · 4 > 359 · 3;
Данное неравенство верно, так как больше то произведение, где больше множители.
1) 170 · 5 + 8 · 5 > 169 · 5 + 6 · 5;
Данное неравенство верно, так как больше то произведение, где больше множители.
2) 6 102 · (81 : 81) > 6 102 · (81 – 81);
Частное чисел 81 и 81 равняется 1, а разность чисел 81 и 81 равняется 0. Соответственно, выражение слева больше.
3) 676 : 4 < 676 : 2;
Данное неравенство верно, так как больше то частное, где меньше делитель.
4) 359 · 4 > 359 · 3;
Данное неравенство верно, так как больше то произведение, где больше множители.
Номер задания: Ребус
Решение:
1) Рассмотрим ребус:
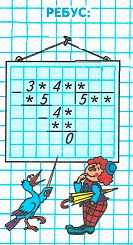 2) Разгадаем ребус:
2) Разгадаем ребус:
1. Подумаем, какое двузначное число с 3 десятками делится на число 5 без остатка. Частное чисел 35 и 5 равняется 7. Значит, на месте сотен в делимом необходимо писать цифру 5. Следовательно, на месте делителя необходимо писать цифру 7, а на месте десятков в частном – цифру 0.
2. Подумаем, какое двузначное число с четырьмя десятками делится на 7 без остатка. Частное чисел 49 и 7 равняется 7. Следовательно, на месте единиц в частном необходимо писать цифру 7.
3. Значит, начальный ребус примет следующий вид:
3 549 : 7 = 507;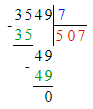

1. Подумаем, какое двузначное число с 3 десятками делится на число 5 без остатка. Частное чисел 35 и 5 равняется 7. Значит, на месте сотен в делимом необходимо писать цифру 5. Следовательно, на месте делителя необходимо писать цифру 7, а на месте десятков в частном – цифру 0.
2. Подумаем, какое двузначное число с четырьмя десятками делится на 7 без остатка. Частное чисел 49 и 7 равняется 7. Следовательно, на месте единиц в частном необходимо писать цифру 7.
3. Значит, начальный ребус примет следующий вид:
3 549 : 7 = 507;
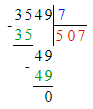
Ответ:
3 549 : 7 = 507.
Страница 91. Что узнали. Чему научились. Номер: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, задача на полях.



