Страница 87, ГДЗ по математике за 4 класс к учебнику Моро часть 1
Страница 87
Краткое условие: Сократи текст в кавычках, не решая задачу.
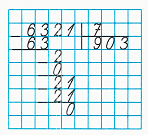
2. Делю десятки. Неполное частное чисел 2 и 7 равняется 0 – столько десятков будет в частном. Умножу 0 на 7, получу 0 – столько десятков разделили. Вычту 0 из 2, получу 2 – столько десятков осталось разделить.
3. Делю единицы. 2 десятка и 1 единица – это 21 единица. Частное чисел 21 и 7 равняется 3. Умножу 3 на 7, получу 21 – столько единиц разделили. Вычту 21 из 21, получу 0. Разделили все единицы.
4. Читаю ответ: 903.
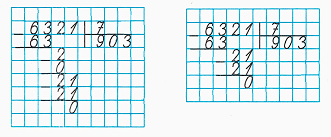
2) Сравним подробную и более краткую записи:
Краткое условие: Вычислим.
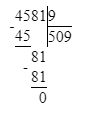
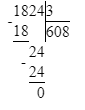
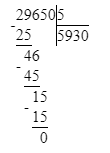
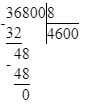
1) 4 581 : 9 = 509;
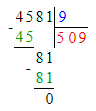
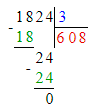
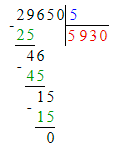
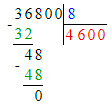
Краткое условие: Назови неверные решения
Значит, 73 сот. — это первое неполное делимое и в записи частного будет 3 цифры.
Деление выполнено неверно, должно быть так:
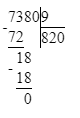
Значит, 30 сот. — это первое неполное делимое и в записи частного будет 3 цифры.
Деление выполнено неверно, должно быть так:
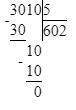
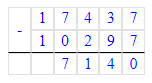
Значит, 56 тыс. — это первое неполное делимое и в записи частного будет 4 цифры.
Деление выполнено верно:
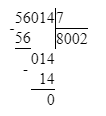
1. В первом примере первое неполное делимое – сотни, а значит в частном будет 3 цифры, а в числе 82 две цифры. Следовательно, первый пример решён неверно.
2. Во втором примере первое неполное делимое – сотни, а значит в частном будет 3 цифры, а в числе 62 две цифры. Следовательно, второй пример решён неверно.
3. В третьем примере первое неполное делимое – тысячи, а значит в частном будет 4 цифры, и в числе 8 002 четыре цифры. Следовательно, третий пример решён верно.
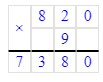
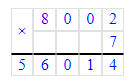
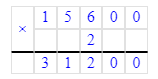
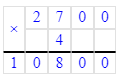
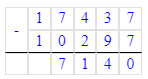
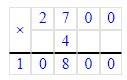
2) Решим правильно и выполним проверку умножением:
1) 7 380 : 9 = 820;
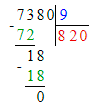
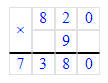
820 · 9 = 7 380;
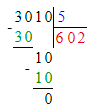
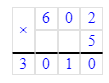
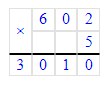
602 · 5 = 3 010;
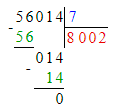
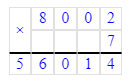
8 002 · 7 = 56 014;
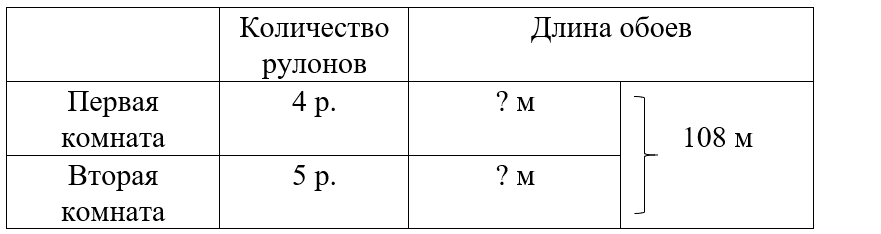
Краткое условие: Чем похожи и чем различаются задачи и их решения? 1) На две комнаты ушло 108 м обоев: на одну — 4 рулона, на другую — 5 рулонов. Сколько метров ушло на каждую? 2) На две комнаты ушло 9 одинаковых рулонов: на одну — 48 м, на другую — 60 м. Сколько рулонов ушло на каждую?
Они похожи тем, что первое действие сложение, второе деление.
Различаются тем, что в 1 – й задаче находим сколько метров обоев, пошло на каждую комнату, а во 2-й задаче – сколько рулонов обоев пошло на каждую комнату.
1)
1 комната – 4 рулона обоев;
2 комната – 5 рулонов обоев;
На каждую комнату - ? м обоев
2) 108÷9=12 (м)- обоев в 1 рулоне;
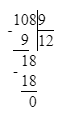
4) 5∙12=60 (м)-обоев ушло на 2-ю комнату.
1 комната – 48 м обоев;
2 комната – 60 м обоев;
На каждую комнату -? рулонов обоев
2) 108÷9=12 (м)- обоев в рулоне;
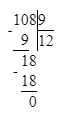
4) 60÷12=5 (рулонов)-обоев ушло на оклейку 2 комнаты.
1.
1) 4 + 5 = 9 р. – всего
Шаг 2. Найдём длину 1 рулона:
2) 108 : 9 = 12 м – длина 1 рулона обоев
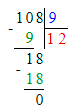
3) 12 · 4 = 48 м – пошло на 1 комнату
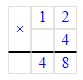
4) 12 · 5 = 60 м – пошло на 2 комнату
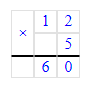
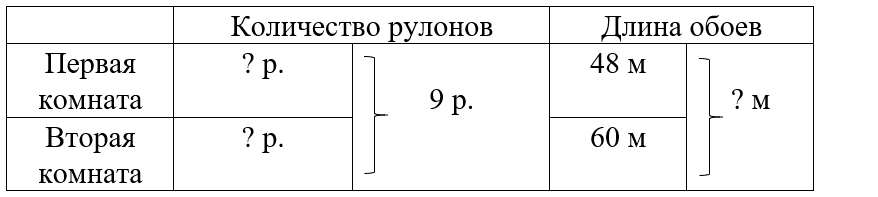
1) 48 + 60 = 108 м – всего
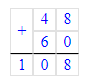
2) 108 : 9 = 12 м – длина 1 рулона обоев
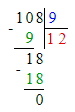
3) 48 : 12 = 4 р. – пошло на 1 комнату
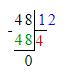
4) 60 : 12 = 5 р. – пошло на 2 комнату
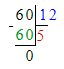
Данные задачи являются обратными. Искомые данные в первой задаче находятся с помощью умножения, а второй задаче – с помощью деления.
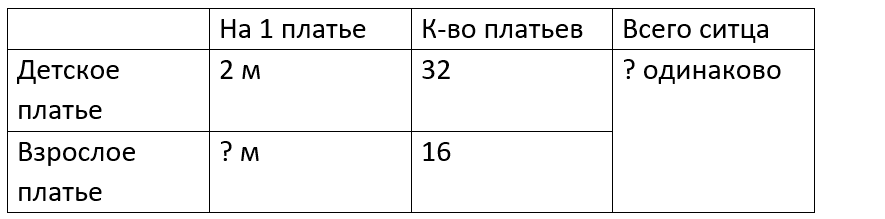
Краткое условие: Из куска ситца можно сшить 32 детских или 16 взрослых платьев. На детское платье идёт 2 м. Сколько метров идёт на взрослое?
2) 64÷16=4 (м)- ситца ушло на взрослое платье.
ШАГ 1. Найти общее количество ситца.
ШАГ 2. Найти расход ситца на 1 платье для взрослых.

1) 32 · 2 = 64 м – всего
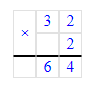
2) 64 : 16 = 4 м – расход на 1 платье для взрослых
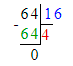
2) 64 : 16 = 4 (м)
Ответ: на каждое платье для взрослых идёт 4 м ситца.
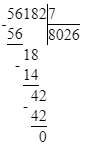
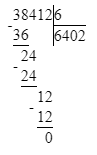
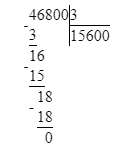
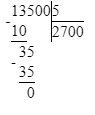
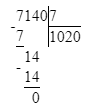

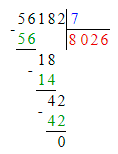
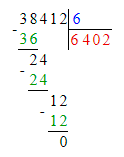

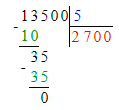
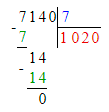
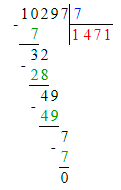
Краткое условие: Найди периметр квадрата со стороной 3 см 2 мм.
Периметр квадрата - ?
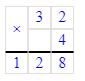
ШАГ 1. Найти длину стороны квадрата в миллиметрах.
ШАГ 2. Найти периметр квадрата.

1) 3 см 2 мм = 32 мм – сторона квадрата
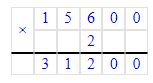
Шаг 2. Найдём периметр квадрата:
2) Р = 32 · 4 = 128 мм = 12 см 8 мм – периметр квадрата
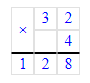
2) Р = 32 · 4 = 128 мм = 12 см 8 мм;
Ответ: периметр квадрата равен 12 см 8 мм.

Так как Петров на 3 года старше Денисова, то Денисов младше всех.
Светлов старше Денисова на: 8+3=11 (лет).
Самым младшим является Денисов.
2) Подумаем, на сколько лет Светлов старше Денисова:
8 + 3 = 11 л.;
Краткое условие: Найди длину стороны квадрата, периметр которого равен 432 мм.
ШАГ 1. Найти длину стороны квадрата.

1) 432 : 4 = 108 мм = 10 см 8 мм – сторона квадрата
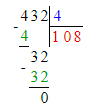
Ответ: сторона квадрата равна 10 см 8 мм.
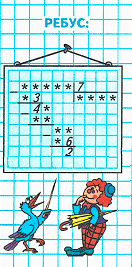
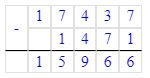
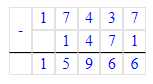
1. Сумма чисел 3 и 4 равняется 7. Значит, на месте единиц тысяч в делимом необходимо писать цифру 7. Подумаем, какое двузначное число с тремя единицами делится на 7 без остатка. Частное чисел 63 и 7 равняется 9. Следовательно, на месте десятков тысяч в делителе необходимо писать число 6, а на месте единиц тысяч в частном – число 9.
2. Подумаем, какое двузначное число с четырьмя десятками делится на 7 без остатка. Частное чисел 49 и 7 равняется 7. Следовательно, на месте сотен в делителе необходимо писать число 9, а на месте сотен в частном – число 7.
3. На месте десятков в частном необходимо писать цифру 0. Сумма чисел 6 и 2 равняется 8. Следовательно, на месте единиц в частном необходимо писать цифру 8.
4. Частное чисел 56 и 7 равняется 8. Значит, на месте десятков в делимом нужно писать число 5, а на месте единиц в частном – цифру 8.
5. Значит, начальный ребус примет следующий вид:
67 958 : 7 = 9 708 (ост. 2);
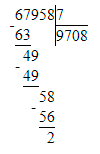
Страница 87. Номер: 408, 409, 410, 411, 412, 413, 414, задача на полях.



