Страница 86, ГДЗ по математике за 4 класс к учебнику Моро часть 1
Страница 86
Краткое условие: Два куска одинаковой ткани стоят 360 р.: один 5 м, другой 4 м. Сколько стоит каждый?
В 1-м куске – 5 м;
Во 2-м куске – 4 м;
1 кусок -? р.
2 кусок -? р.
2) 360÷9=40 (р.)- стоит 1 м ткани;
3) 40∙5=200 (р)- стоит 1 - й кусок ткани;
4) 4∙40=160 (р)- стоит 2 - й кусок ткани.
ШАГ 1. Найти общее количество ткани.
ШАГ 2. Найти стоимость 1 м ткани.
ШАГ 3. Найти стоимость первого куска.
ШАГ 4. Найти стоимость второго куска.
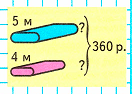
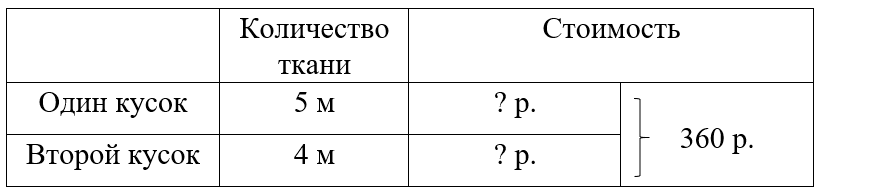
1) 5 + 4 = 9 м – всего
Шаг 2. Найдём стоимость 1 м ткани:
2) 360 : 9 = 40 р. – стоит 1 м
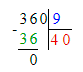
3) 40 · 5 = 200 р. – стоимость одного куска ткани
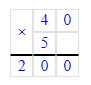
4) 40 · 4 = 160 р. – стоимость второго куска ткани
2) 360 : 9 = 40 (р.)
3) 40 · 5 = 200 (р.)
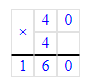
4) 40 · 4 = 160 (р.)
Ответ: стоимость одного куска ткани равна 200 р.; стоимость второго куска ткани равна 160 р.
Краткое условие: В одном мешке было 56 кг муки, в другом — 24 кг. Всю муку поровну расфасовали в 40 пакетов. Сколько пакетов потребовалось для каждого мешка?

2) 80÷40=2 (кг)- муки в 1-м пакете;
3) 56÷2=28 (пакетов)- потребовалось для расфасовки муки из 1-го мешка;
4) 24÷2=12 (пакетов)- потребовалось для расфасовки муки из 2-го мешка;
ШАГ 1. Найти общее количество муки.
ШАГ 2. Найти сколько муки вмещается в 1 пакет.
ШАГ 3. Найти сколько потребовалось пакетов для первого мешка.
ШАГ 4. Найти сколько потребовалось пакетов для второго мешка.
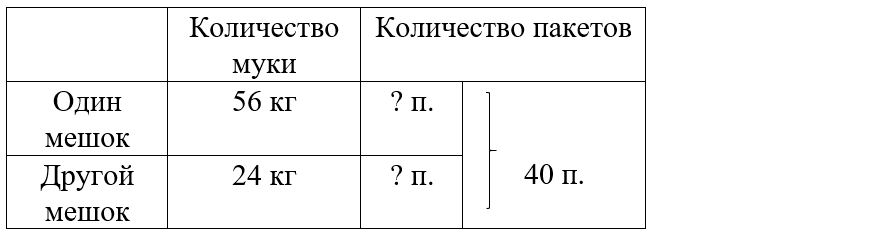
1) 56 + 24 = 80 кг – всего
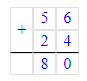
2) 80 : 40 = 2 кг – в 1 пакете
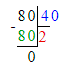
3) 56 : 2 = 28 п. – для 1 мешка
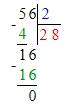
4) 24 : 2 = 12 п. – для 2 мешка
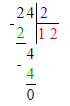
2) 80 : 40 = 2 (кг)
3) 56 : 2 = 28 (п.)
4) 24 : 2 = 12 (п.)
Ответ: для расфасовки 1 мешка потребовалось 28 пакетов; для расфасовки 2 мешка потребовалось 12 пакетов.
Краткое условие: Определи заранее число цифр в частном и выполни деление.
6 336÷2=3 168;
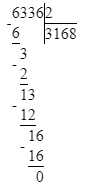
6 336÷9=704;
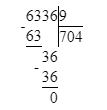
58 135÷7=8 305;
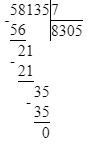
34 472÷8=4 309;
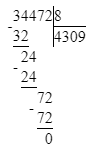
251 052÷6=41 842;
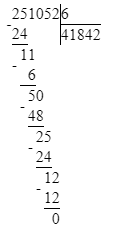
411 258÷3=137 086;

136 012÷4=34 003;
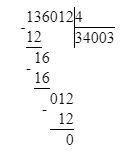
254 105÷5=50 821.
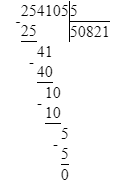
1) 6 336 : 2 = 3 168;
Делю тысячи. 6 тысяч – это первое неполное делимое. Значит, в частном получатся тысячи и в записи частного будет 4 цифры.
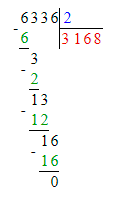
Делю сотни. 63 сотни – это первое неполное делимое. Значит, в частном получатся сотни и в записи частного будет 3 цифры.
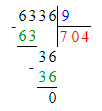
Делю тысячи. 58 тысяч – это первое неполное делимое. Значит, в частном получатся тысячи и в записи частного будет 4 цифры.
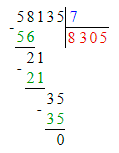
Делю тысячи. 34 тысячи – это первое неполное делимое. Значит, в частном получатся тысячи и в записи частного будет 4 цифры.
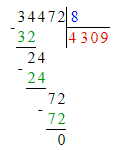
Делю десятки тысяч. 25 десятков тысяч – это первое неполное делимое. Значит, в частном получатся десятки тысяч и в записи частного будет 5 цифр.
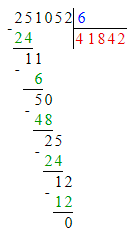
Делю сотни тысяч. 4 сотни тысяч – это первое неполное делимое. Значит, в частном получатся сотни тысяч и в записи частного будет 6 цифр.
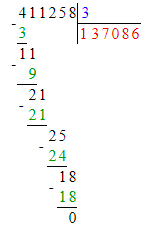
Делю десятки тысяч. 13 десятков тысяч – это первое неполное делимое. Значит, в частном получатся десятки тысяч и в записи частного будет 5 цифр.
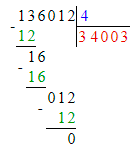
Делю десятки тысяч. 25 десятков тысяч – это первое неполное делимое. Значит, в частном получатся десятки тысяч и в записи частного будет 5 цифр.
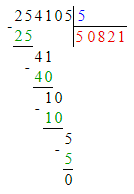
Краткое условие: Ребята заполнили два аквариума водой: в один — 300 л, в другой — 312 л. Сколько вёдер воды они принесли?
В 1 ведре - 6 л воды;
Всего - ? ведер
2) 612÷6=102 (ведра)- воды всего пришлось принести.
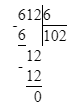
ШАГ 1. Найти общее количество воды.
ШАГ 2. Найти количество вёдер.
Ребята заполнили водой два больших аквариума: в один они влили 300 л воды, а в другой – 312 л. Сколько вёдер воды им пришлось принести, если вместимость одного ведра равняется 6 л?
2) Решим задачу:

1) 300 + 312 = 612 л – всего
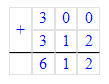
2) 612 : 6 = 102 в. – понадобится
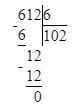
2) 612 : 6 = 102 (в.)
Ответ: понадобится 102 ведра.
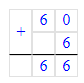
1 мин 6 с=(1∙60)с+6 с=66 с;
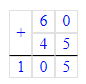
1 ч 45 мин=(1∙60)мин+45 мин=105 мин;
2 355 кг=2 т 355 кг;
62 335 кг=62 т 335 кг;
584 мм=58 см 4 мм.
2) 1 мин 6 с = 60 с + 6 с = 66 с;
5) 62 335 кг = 62 т 335 кг;
6) 584 мм = 58 см 4 мм;
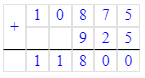
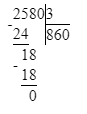
10 км 875 м = 10 875 м;

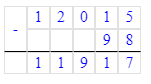
2) 12 т 015 кг – 98 кг = 11 т 917 кг;
12 т 015 кг = 12 015 кг;

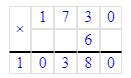
3) 17 м 30 см · 6 = 103 м 80 см;
17 м 30 см = 1 730 см;

4) 25 ц 80 кг : 3 = 8 ц 60 кг;
25 ц 80 кг = 2 580 кг;
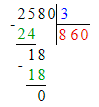
Краткое условие: Реши только уравнения, где неизвестное находится делением.
x∙5=4 500
x=4 500÷5
x=900
x=6 800÷100
x=68
x=7 000÷100
x=70
x-0=999- не подходит данное уравнение.
1) х · 5 = 4 500;
х = 4 500 : 5;
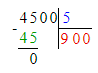
2) 100 · х = 6 800;
х = 6 800 : 100;
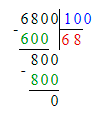
3) 7 000 : х = 100;
х = 7 000 : 100;
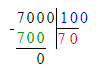
Краткое условие: Вычислим и выполним проверку.
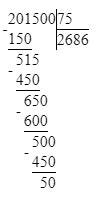
1) 50<75
2) 2686∙75=201 450
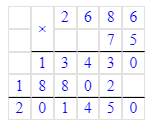
25 600÷78=328 (ост.16);
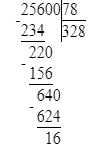
1) 16<78
2) 328∙78=25 584
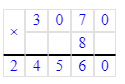
3 070∙8=24 560.
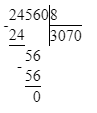
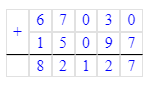
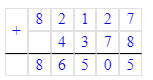
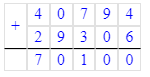
67 030+15 097+4 378=86 505;
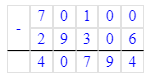
70 100-29 306=70 100.
1)
1. 201 500 : 5 = 40 300;
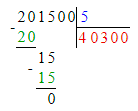
40 300 · 5 = 201 500;
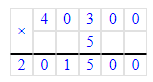
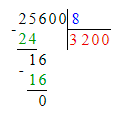
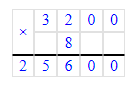
3 200 · 8 = 25 600;
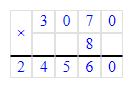
24 560 : 8 = 3 070;
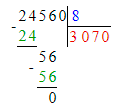
1. 67 030 + 15 097 + 4 378 = 82 127 + 4 378 = 86 505;


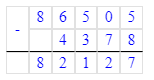
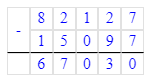
86 505 - 4 378 - 15 097 = 82 127 - 15 097 = 67 030;



40 794 + 29 306 = 70 100;

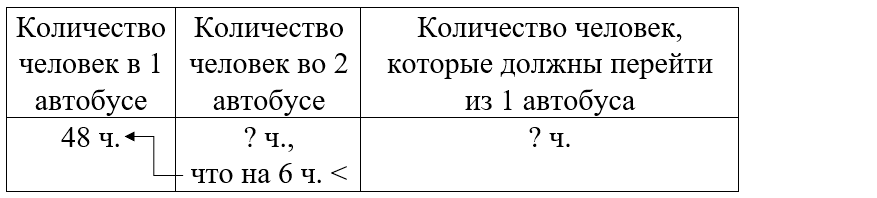
Краткое условие: Во время экскурсии в первый автобус сели 48 человек, во второй — на 6 меньше. Сколько человек должны перейти из первого автобуса во второй для равного числа пассажиров?

2) 48+42=90 (чел.)- в 2-х автобусах всего;
3) 90÷2=45 (чел)-должно быть в автобусах;
4) 48-45=3 (чел)- должны перейти во 2-й автобус из 1-го, чтобы их в обоих автобусах было поровну.
ШАГ 1. Найти количество человек во 2 автобусе.
ШАГ 2. Найти общее количество человек в 2 автобусах.
ШАГ 3. Найти количество человек в каждом автобусе, если бы в них было одинаковое количество человек.
ШАГ 4. Найти количество человек, которые должны перейти из первого автобуса во второй, чтобы в них пассажиров стало поровну.
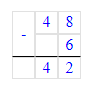
1) 48 - 6 = 42 ч. – во 2 автобусе
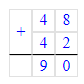
2) 48 + 42 = 90 ч. – в 2 автобусах
3) 90 : 2 = 45 ч. – в каждом автобусе
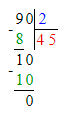
4) 45 - 42 = 3 ч. – столько человек должно перейти
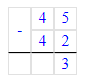
2) 48 + 42 = 90 (ч.)
3) 90 : 2 = 45 (ч.)
4) 45 - 42 = 3 (ч.)
Ответ: должны перейти 3 человека.
Краткое условие: Вычислим.
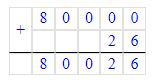
1) 8 м2 26 дм2 + 72 дм2 = 8 м2 98 дм2;
8 м2 26 дм2 = 80 000 дм2 + 26 дм2 = 80 026 дм2;
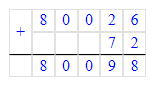
2) 9 см 2 мм · 5 = 60 с + 6 с = 46 см;
9 см 2 мм = 92 мм;
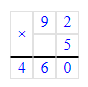
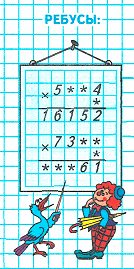
1)
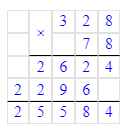
1. Подумаем, при произведении какого числа на число 4 в единицах частного будет цифра 2. Произведение чисел 4 и 3 равняется 12. Следовательно, на месте второго множителя нужно писать цифру 3. 12 единиц – это 1 десяток и 2 единицы. 1 десяток запоминаем.
2. Разность чисел 25 и 1 равняется 24. Частное чисел 24 и 3 равняется 8. Следовательно, на месте десятков первого множителя необходимо писать цифру 8. 25 десятков – это 2 сотни и 5 десятков. 2 сотни запоминаем.
3. Разность чисел 11 и 2 равняется 9. Частное чисел 9 и 3 равняется 3. Значит, на месте сотен первого множителя необходимо писать цифру 3. 11 сотен – это 1 тысяча и 1 сотня. 1 тысячу запоминаем.
4. Произведение чисел 5 и 3 равняется 15. Сумма чисел 15 и 1 равняется 16.
5. Значит, начальный первый ребус примет следующий вид:
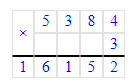
5 384 · 3 = 16 152;
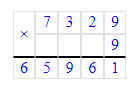
1. Подумаем, при произведении каких чисел в единицах частного будет цифра 1. Произведение чисел 9 и 9 равняется 81. Следовательно, на месте единиц первого множителя и на месте второго множителя нужно писать цифру 9. 81 единица – это 8 десятков и 1 единица. 1 десяток запоминаем.
2. Разность чисел 26 и 8 равняется 18. Частное чисел 18 и 9 равняется 2. Следовательно, на месте десятков первого множителя необходимо писать цифру 2. 26 десятков – это 2 сотни и 6 десятков. 2 сотни запоминаем.
3. Произведение чисел 3 и 9 равняется 27. Сумма чисел 27 и 2 равняется 29. 29 сотен – это 2 тысячи и 9 сотен. Значит, на месте сотен частного необходимо писать цифру 9. 2 тысячи запоминаем.
4. Произведение чисел 7 и 9 равняется 63. Сумма чисел 63 и 2 равняется 65. Цифру 5 нужно писать в разряде единиц тысяч, а цифру 6 – в разряде десятков тысяч.
5. Значит, начальный второй ребус примет следующий вид:
7 329 · 9 = 65 961;
Страница 86. Номер: 399, 401, 402, 403, 404, 405, 406, 407, задача на полях.



