ГДЗ 4 класс Математика Моро, Бантова, Бельтюкова

4класс

Страница 79, ГДЗ по математике за 4 класс к учебнику Моро часть 1

Выберите номер:

Задача на полях 354 355 356 357 358 359 360 Задача на полях Ребус

Номер задания: Задача на полях

Краткое условие: Объясни, как выполнено умножение.

Решение:

1) Рассмотрим записи и объясним вычисления:

1. Произведение восьми сотен и числа 7 равняется 56 сотен. 56 сотен – это 5 600 единиц. Следовательно, произведение чисел 800 и 7 равняется 5 600.
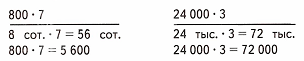
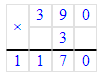
2. Произведение двадцати четырёх тысяч и числа 3 равняется 72 тысячи. 72 тысячи – это 72 000 единиц. Следовательно, произведение чисел 24 000 и 3 равняется 72 000.
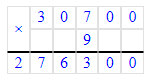
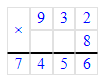
2) Объясним, как выполнено умножение:

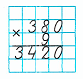
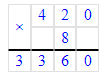
1) Произведение чисел 0 и 9 равняется 0. В разряде единиц пишем 0.
2) Произведение чисел 8 и 9 равняется 72. 72 десятка – это 7 сотен и 2 десятка. В разряде десятков пишем 2, 7 сотен запоминаем.
3) Произведение чисел 3 и 9 равняется 27. Сумма чисел 27 и 7 равняется 34. 34 сотни – это 3 тысячи и 4 сотни. В разряде сотен пишем 4, а в разряде единиц тысяч - 3.

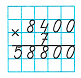
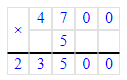
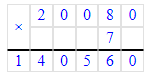
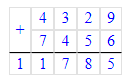
1) Произведение чисел 0 и 7 равняется 0. В разряде единиц и десятков пишем 0.
2) Произведение чисел 4 и 7 равняется 28. 28 сотен – это 2 тысячи и 8 сотен. В разряде сотен пишем 8, а 2 тысячи запоминаем.
3) Произведение чисел 8 и 7 равняется 56. Сумма чисел 56 и 2 равняется 58. 58 тысяч – это 5 десятков тысяч и 8 единиц тысяч. В разряде единиц тысяч пишем 8, а в разряде десятков тысяч - 5.

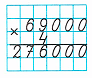
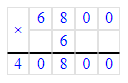
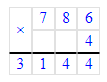
1) Произведение чисел 0 и 4 равняется 0. В разряде единиц, десятков и сотен пишем 0.
2) Произведение чисел 9 и 4 равняется 36. 36 тысяч – это 3 десятка тысяч и 6 единиц тысяч. В разряде единиц тысяч пишем 6, а 3 десятка тысяч запоминаем.
3) Произведение чисел 6 и 4 равняется 24. Сумма чисел 24 и 3 равняется 27. В разряде десятков тысяч пишем 7, а в разряде сотен тысяч - 2.

Номер задания: 354

Решение:

420∙8=3 360;

390∙3=1 170;

4 700∙5=23 500;

6 800∙6=40 800;

30 700∙9=276 300;

20 080∙7=140 560;

5 000 - 786 ∙ 4=1 856;

4 329 + 932 ∙ 8=11 785.

Решение:

1) 420∙8=3 360;

2) 390∙3=1 170;

3) 4 700∙5=23 500;

4) 6 800∙6=40 800;

5) 30 700∙9=276 300;

6) 20 080∙7=140 560;

7) 5 000 - 786 ∙ 4=1 856;

8) 4 329 + 932 ∙ 8=11 785.

Ответ:

1) 3 360; 2) 1 170; 3) 23 500; 4) 40 800; 5) 276 300; 6) 140 560; 7) 1 856; 8) 11 785.

Номер задания: 355

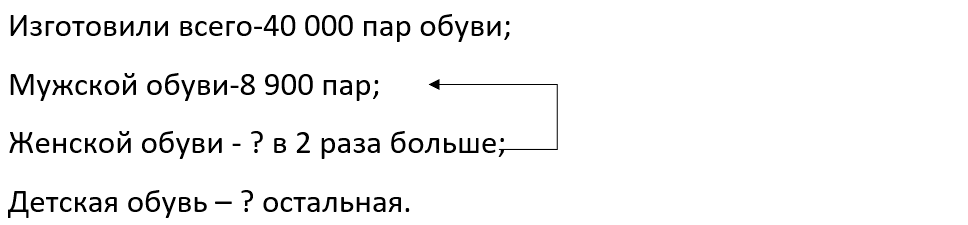
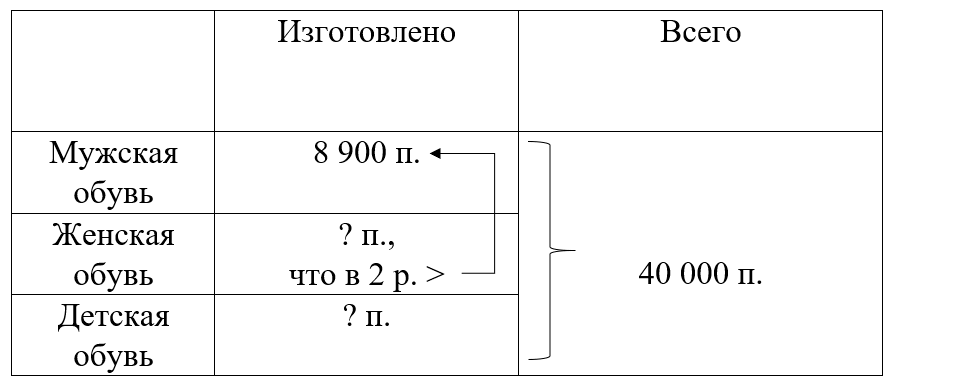
Краткое условие: На фабрике за месяц изготовили 40 000 пар обуви: мужской — 8 900 пар, женской — в 2 раза больше, остальная — детская. Сколько пар детской обуви изготовили?

Дано:

Решение:

1) 8 900∙2=17 800 (пар)- женской обуви изготовили за месяц;

2) 8 900+17 800=26 700 (пар)- мужской и женской обуви изготовили за месяц;

3) 40 000-26 700=13 300 (пар)- детской обуви изготовили.

Ответ:

13 300 пар детской обуви.

Подсказка

Чтобы решить задачу, нужно:
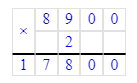
ШАГ 1. Найти сколько изготовили женской обуви.
ШАГ 2. Найти сколько изготовили мужской и женской обуви вместе.
ШАГ 3. Найти сколько изготовили детской обуви.

Дано:

Решение:

Шаг 1. Найдём сколько изготовили женской обуви:
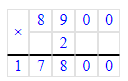
1) 8 900 · 2 = 17 800 п. – женская обувь

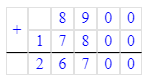
Шаг 2. Найдём сколько изготовили женской и мужской обуви вместе:
2) 8 900 + 17 800 = 26 700 п. – женская и мужская обувь

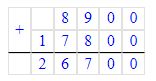
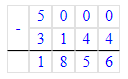
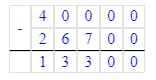
Шаг 3. Найдём сколько изготовили детской обуви:
3) 40 000 – 26 700 = 13 300 п. – детская обувь

Ответ:

за месяц изготовили 13 300 пар детской обуви.

Под запись в тетрадь:

1) 8 900 · 2 = 17 800 (п.)
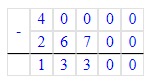
2) 8 900 + 17 800 = 26 700 (п.)
3) 40 000 – 26 700 = 13 300 (п.)
Ответ: за месяц изготовили 13 300 пар детской обуви.

Номер задания: 356

Краткое условие: На завод привезли 80 машин свёклы по 3 т в каждой. Сколько сахара изготовили, если масса сахара — шестая часть массы свёклы?

Дано:

80 машин свеклы по 3 т в каждой;
Масса сахара – шестую часть массы свеклы;
Сахара -? т

Решение:

1) 80∙3=240 (т)- свеклы привезли на завод;
2) 240÷6=40 (т)- сахара изготовили.

Ответ:

40 т сахара.

Подсказка

Чтобы решить задачу, нужно:
ШАГ 1. Найти массу всей свёклы.
ШАГ 2. Найти сколько сахара изготовили из всей свёклы.

Дано:

Решение:

Шаг 1. Найдём массу всей свёклы:
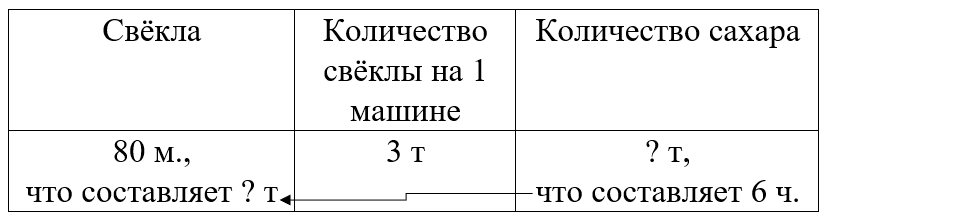
1) 80 · 3 = 240 т – всего свёклы

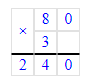
Шаг 2. Найдём сколько сахара изготовили из всей свёклы:
2) 240 : 6 = 40 т – сахар

Ответ:

изготовили 40 т сахара.

Под запись в тетрадь:

1) 80 · 3 = 240 (т)
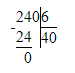
2) 240 : 6 = 40 (т)
Ответ: изготовили 40 т сахара.

Номер задания: 357

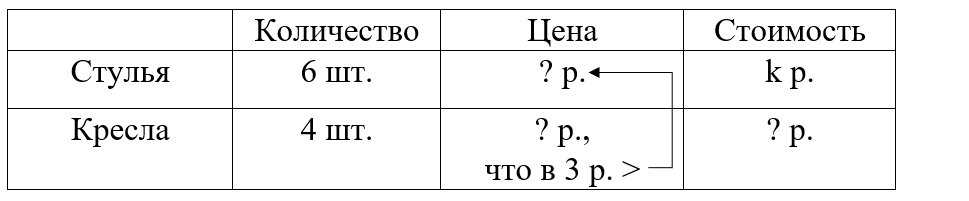
Краткое условие: Купили 6 стульев за к р. Сколько стоят 4 кресла, если каждое в 3 раза дороже стула? Запиши решение выражением.

Дано:

Стульев – 6 за k р.;
Кресел – 4, если каждое в 3 раза дороже стула;
4 кресла -? р.

Решение:

1) k÷6 (р.)- стоит 1 стул;
2) 3∙(k÷6) (р.)- стоит 1 кресло;
3) k÷6∙3∙4 (р.)- стоит 4 кресла.

Ответ:

k÷6∙3∙4 рублей.

Подсказка

Чтобы решить задачу, нужно:
ШАГ 1. Найти цену одного стула.
ШАГ 2. Найти цену одного кресла.
ШАГ 3. Найти стоимость 4 кресел.

Дано:

Решение:

Шаг 1. Найдём цену одного стула:
1) k : 6; – цена 1 стула
Шаг 2. Найдём цену одного кресла:
2) 3 · (k : 6); – цена 1 кресла
Шаг 3. Найдём стоимость 4 кресел:
3) 4 · 3 · (k : 6) = 12 · (k : 6); – стоимость 4 кресел

Ответ:

стоимость 4 кресел равна 12 · (k : 6).

Под запись в тетрадь:

1) k : 6;
2) 3 · (k : 6);
3) 4 · 3 · (k : 6) = 12 · (k : 6);
Ответ: стоимость 4 кресел равна 12 · (k : 6).

Номер задания: 358

Краткое условие: Найди остаток и проверь вычисления.

Решение:

789÷8=98 (ост.5)

Проверка:
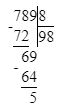
1) 5<8
2) 98∙8=784

3) 784+5=789.

39÷40=0(ост.39)
Проверка:
1) 39<40
2) 40∙0=0
3) 0+39=39.

327÷6=54 (ост.3)

Проверка:
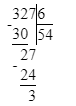
1) 3<6
2) 54∙6=324

3) 324+3=327.

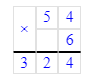
97÷95=1 (ост.2)
Проверка:
1) 2<95
2) 95∙1=95
3) 95+2=97.

Решение:

Найдем остаток и проверим вычисления:
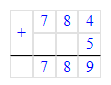
1) 789 : 8 = 98 (ост. 5)

Проверка:
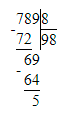
1) 5 < 8;
2) 98 · 8 = 784;

3) 784 + 5 = 789;

2) 39 : 40 = 0 (ост. 39)
Проверка:
1) 39 < 40;
2) 0 · 40 = 0;
3) 0 + 39 = 39;
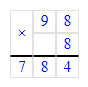
3) 327 : 6 = 54 (ост. 3)

Проверка:
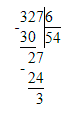
1) 3 < 6;
2) 54 · 6 = 324;

3) 324 + 3 = 327;

4) 97 : 95 = 1 (ост. 2)

Проверка:
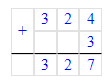
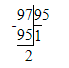
1) 2 < 95;
2) 1 · 95 = 95;
3) 95 + 2 = 97;

Ответ:

1) 98 (ост. 5); 2) 0 (ост. 39); 3) 54 (ост. 3); 4) 1 (ост. 2).

Номер задания: 359

Краткое условие: Вырази: 1) в минутах; 2) в секундах; 3) в килограммах.

Решение:

1)
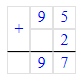
3 ч 45 мин=(3∙60)мин+45 мин=225 мин;
6 ч 40 мин=(6∙60)мин+40 мин=400 мин.
2)
5 мин 05 с=(5∙60)с+5 с=305 с;
10 мин=(10∙60)с=600 с.
3)
6 ц=600 кг;
15 т=15 000 кг;
7 000 г=7 кг.

Решение:

Выразим:
1) в минутах:
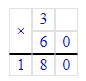
1. 3 ч 45 мин = 3 · 60 мин + 45 мин = 180 мин + 45 мин = 225 мин;

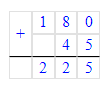
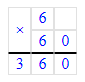
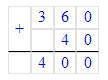
2. 6 ч 40 мин = 6 · 60 мин + 40 мин = 360 мин + 40 мин = 400 мин;

2) в секундах:
1. 5 мин 05 с = 5 · 60 с + 5 с = 300 с + 5 с = 305 с;

2. 10 мин = 10 · 60 с = 600 с;

3) в килограммах:
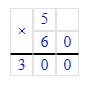
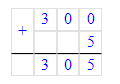
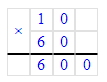
1. 6 ц = 6 · 100 кг = 600 кг;

2. 15 т = 15 · 1 000 кг = 15 000 кг;

3. 7 000 г = 7 кг;

Ответ:

1) 225 мин; 400 мин; 2) 305 с; 600 с; 3) 600 кг; 15 000 кг; 7 кг.

Номер задания: 360

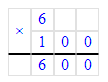
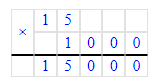
Краткое условие: «Если сажать по 9 на дом — не хватит 100, если по 5 — останется 20. Сколько домов и саженцев?»

Дано:

Решение:

1) 9-5=на 4 (саженца)- меньше посадили у каждого дома во 2-м случае;
2) 100+20=на 120 (саженцев)- меньше посадили всего во 2-м случае;
3) 120÷4=30 (домов)- было всего;
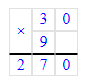
4) 30∙9-100=270-100=170 (саженцев)-было всего.

Ответ:

30 домов, 170 саженцев.

Подсказка

Чтобы решить задачу, нужно:
ШАГ 1. Найти разницу в количестве саженцев для двух способов.
ШАГ 2. Найти количество саженцев для найденной разницы.
ШАГ 3. Найти количество домов.
ШАГ 4. Найти количество саженцев.

Дано:

Решение:

Шаг 1. Найдём разницу в саженцах на 1 дом:
1) 9 – 5 = 4 с. – разница
Шаг 2. Найдём количество саженцев для данной разницы:
2) 100 + 20 = 120 с. – саженцы

Шаг 3. Найдём сколько было домов:
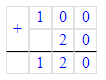
3) 120 : 4 = 30 д. – количество домов

Шаг 4. Найдём сколько было саженцев:
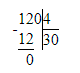
4) 30 · 9 - 100 = 270 – 100 = 170 с. – количество саженцев

Ответ:

было 30 домов; было 170 саженцев.

Под запись в тетрадь:

1) 9 – 5 = 4 (с.)
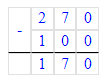
2) 100 + 20 = 120 (с.)
3) 120 : 4 = 30 (д.)
4) 30 · 9 - 100 = 170 (с.)
Ответ: было 30 домов; было 170 саженцев.

Номер задания: Задача на полях

Решение:

Вычислим:
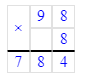
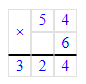
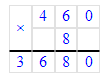
1) 460 · 8 = 3 680;

2) 7 320 · 5 = 36 600;

Ответ:

1) 3 680; 2) 36 600.

Номер задания: Ребус

Решение:

1) Рассмотрим ребус:

2) Разгадаем ребус:
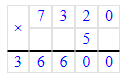
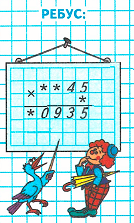
1. Произведение чисел 5 и 3 равняется 15. Следовательно, на месте второго множителя нужно писать цифру 3. 15 единиц – это 1 десяток и 5 единиц. 1 десяток запоминаем.
2. Произведение чисел 4 и 3 равняется 12. Сумма чисел 12 и 1 равняется 13. 13 десятков – это 1 сотня и 3 десятка. 1 сотню запоминаем.
3. Разность чисел 9 и 1 равняется 8. Частное чисел 18 и 3 равняется 6. Значит, на месте сотен первого множителя необходимо писать цифру 6. 18 сотен – это 1 тысяча и 8 сотен. 1 тысячу запоминаем.
4. Разность чисел 10 и 1 равняется 9. Частное чисел 9 и 3 равняется 3. Значит, на месте единиц тысяч первого множителя необходимо писать цифру 3. Пишу 1 в разряд десятков тысяч.
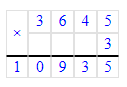
5. Значит, начальный ребус примет следующий вид:
3645 · 3 = 10 935;