Страница 77, ГДЗ по математике за 4 класс к учебнику Моро часть 1
Страница 77
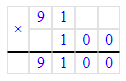
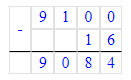
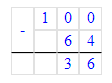
Краткое условие: Объясни, как выполнено умножение.
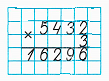
1. Пишу десятки под десятками, сотни под сотнями, единицы под единицами.
2. Умножаем единицы. Произведение чисел 2 и 3 равняется 6. Пишу 6 под единицами.
3. Умножаем десятки. Произведение чисел 3 и 3 равняется 9. Пишу 9 под десятками.
4. Умножаем сотни. Произведение чисел 4 и 3 равняется 12. 12 сотен – это 1 тысяча и 2 сотни. Пишу 2 под сотнями, 1 тысячу запоминаем.
5. Умножаем единицы тысяч. Произведение чисел 5 и 3 равняется 15. Сумма чисел 15 и 1 равняется 16. Пишу 6 под единицами тысяч, а 1 записываем в разряд десятков тысяч.
6. Читаю ответ: 16 296.
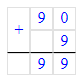
Краткое условие: Выполни умножение, используя перестановку множителей.
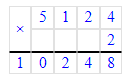
5 124∙2=10 248;
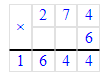
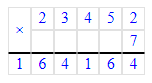
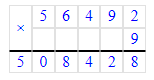
2 км 425 м∙8=2 425 м∙8=19 400 м=19 км 400 м;
1)
1. 5 124 · 2 = 10 248;




1. 2 км 425 м · 8 = 19 км 400 м;
2 км 425 м = 2 425 м;

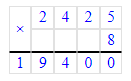
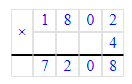
2. 18 ц 02 кг · 4 = 72 ц 8 кг;
18 ц 02 кг = 1 802 кг;

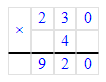
3. 230 см2 · 4 = 920 см2;

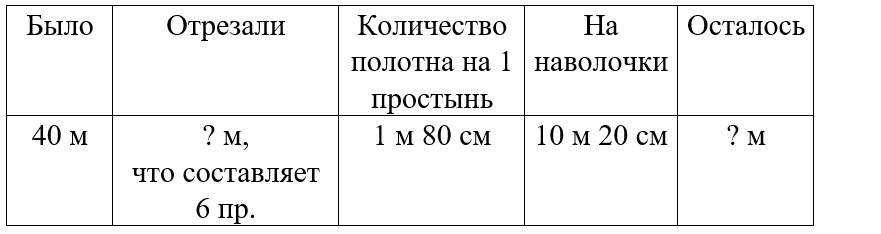
Краткое условие: В куске 40 м полотна. Отрезали на 6 детских простыней по 1 м 80 см и на наволочки 10 м 20 см. Сколько метров осталось?
На 6 простыней - ? по 1 м 80 см на каждую;
На наволочки – 10 м 20 см;
Осталось - ?
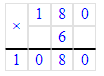
ШАГ 1. Найти сколько метров полотна необходимо на 6 простыней.
ШАГ 2. Найти сколько полотна отрезали на простыни и наволочки.
ШАГ 3. Найти сколько полотна осталось.
1) 1 м 80 см · 6 = 180 см · 6 = 1 080 см – на простыни

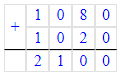
2) 1 080 см + 10 м 20 см = 1 080 см + 1 020 см = 2 100 см = 21 м – отрезали всего

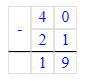
3) 40 - 21 = 19 м – осталось
2) 1 080 см + 10 м 20 см = 21 (м)
3) 40 - 21 = 19 (м)
Ответ: осталось 19 м полотна.
Краткое условие: В мастерской сшили 6 простыней по 2 м 20 см и 8 наволочек по 1 м 25 см.
Сшили 8 наволочек по 1 м 25 см;
Всего-?
ШАГ 1. Найти сколько метров полотна необходимо на 6 простыней.
ШАГ 2. Найти сколько метров полотна необходимо на 8 наволочек.
ШАГ 3. Найти общее количество расходуемого полотна.
В мастерской сшили 6 простыней, расходуя на каждую по 2 м 20 см полотна, и 8 наволочек, расходуя на каждую по 1 м 25 см полотна. Сколько метров полотна ушло на пошив простыней и наволочек?
2) Решим задачу:

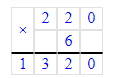
1) 2 м 20 см · 6 = 220 см · 6 = 1 320 см – на простыни

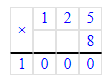
2) 1 м 25 см · 8 = 125 см · 8 = 1 000 см – на наволочки

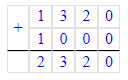
3) 1 320 + 1 000 = 2 320 см = 23 м 20 см – израсходовали
2) 1 м 25 см · 8 = 1 000 (см)
3) 1 320 + 1 000 = 2 320 см = 23 м 20 см
Ответ: всего израсходовали 23 м 20 см полотна.
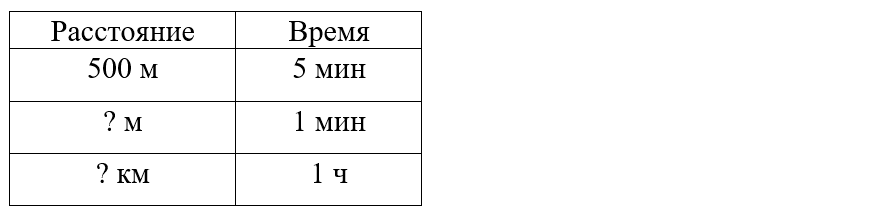
Краткое условие: Папа прошёл 500 м за 5 мин. Сколько км он пройдёт за 1 ч, если скорость постоянна?
За 1 ч -? км
1) 500 м÷5=100 (м)- проходит папа за 1 минуту;
2) 100 м∙60=6 000 (м)=6 (км)- пройдёт папа за 1 час.
ШАГ 1. Найти сколько метров проходит папа за 1 минуту.
ШАГ 2. Перевести часы в минуты.
ШАГ 3. Найти сколько километров проходит папа за 1 час.
1) 500 : 5 = 100 м – за 1 минуту
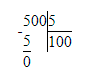
2) 1 ч = 60 мин – время в минутах
Шаг 3. Найдём сколько километров пройдёт папа за 1 час:
3) 60 · 100 = 6 000 м = 6 км – за 1 ч
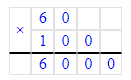
2) 1 ч = 60 мин;
3) 60 · 100 = 6 000 м = 6 (км)
Ответ: за 1 ч папа пройдёт 6 км.


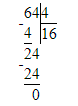


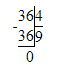
Краткое условие: 1) Сравни площади ABCD и КМОР. 2) Сравни площади ATFD и КОР. 3) Верно ли, что КО — ось симметрии КМОР?
BC=AD= 3 см;
KM=OP= 6 см;
MO=KP= 3 см;
SABCD-?
SKMOP-?
Сравнить SABCD и SKMOP.
SKMOP=6∙3=18 см2;
SABCD = SKMOP.
Прямоугольник ABCD разделён на два равных квадрата, значит: SATFD=18÷2=9 см2.
Прямоугольник KMOP разделён на два равных треугольника,
Значит: SKOP=18÷2=9 см2.
Таким образом, площади квадрата и треугольника равны:
SATFD=SKOP=9 см2.
3)
KO – не является осью симметрии фигуры KMOP.
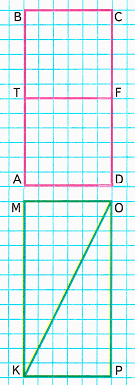
1. Найдем площадь прямоугольника АВСD:
S = АВ · ВС = 6 см · 3 см = 18 см2;
2. Найдем площадь прямоугольника КМОР:
S = КМ · МО = 6 см · 3 см = 18 см2;
3. Сравним полученные результаты:
Так как 18 см2 = 18 см2, то площади прямоугольников АВСD и КМОР равны.
3) Сравним площади квадрата АТFD и треугольника КОР:
1. Найдем площадь квадрата АТFD:
S = АТ · ТF = 3 см · 3 см = 9 см2;
2. Найдем площадь треугольника КОР:
S = (КМ · МО) : 2 = (6 см · 3 см) : 2 = 18 см2 : 2 = 9 см2;
3. Сравним полученные результаты:
Так как 9 см2 = 9 см2, то площади квадрата АТFD и треугольника КОР равны.
4) Подумаем, верно ли, что КО – ось симметрии фигуры КМОР:
Нет, КО не является осью симметрии фигуры КМОР.
Краткое условие: В первой корзине было 25 кг слив, во второй — на 7 кг меньше. Из первой переложили во вторую 4 кг. В какой корзине стало больше слив и на сколько?
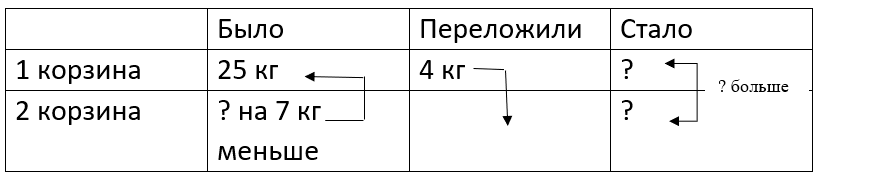
2) 25-4=21 (кг)- слив стало в 1-й корзине;
3) 18+4=22 (кг)- слив стало во 2-й корзине;
4) 22-21= на 1 (кг) – слив стало больше во 2-й корзине, чем в первой.
ШАГ 1. Найти сколько было слив во второй корзине.
ШАГ 2. Найти сколько стало слив в первой корзине.
ШАГ 3. Найти сколько стало слив во второй корзине.
ШАГ 4. Найти в какой корзине слив стало больше и на сколько килограммов.

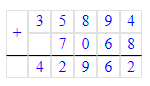
1) 25 - 7 = 18 кг – было во второй корзине
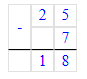
2) 25 - 4 = 21 кг – стало в первой корзине
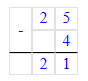
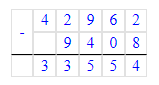
3) 18 + 4 = 22 кг – стало во второй корзине
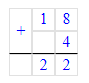
4) 22 - 21 = 1 кг – на столько слив больше во второй корзине
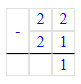
2) 25 - 4 = 21 (кг)
3) 18 + 4 = 22 (кг)
4) 22 - 21 = 1 (кг)
Ответ: во второй корзине стало на 1 кг слив больше, чем в первой.
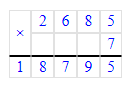
26 м 85 см = 2 685 см;
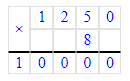
2) 1 т 250 кг · 8 = 10 т;
1 т 250 кг = 1 250 кг;
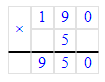
3) 190 мм2 · 5 = 950 мм2;
Страница 77. Номер: 337, 338, 339, 340, 341, 342, 343, задача на полях.



