Страница 64, ГДЗ по математике за 4 класс к учебнику Моро часть 1
Страница 64
Краткое условие: Начерти отрезок 60 мм. Узнай, сколько мм в пяти шестых этого отрезка.
1) 60÷6=10 (мм)- длина одной части;
2) 10∙5=50 (мм)-длина пяти шестых долях отрезка.
60 мм = 6 см;
3) Найдем, сколько сантиметров в пяти шестых долях отрезка:
1 · 5 = 5 (см)
4) Найдем, сколько миллиметров в пяти шестых долях отрезка:
Так как 1 см = 10 мм, то 5 см = 50 мм;
Краткое условие: Начерти прямоугольник, вырежи, разрежь по отрезку, наложением проверь равенство треугольников, найди площадь одного.
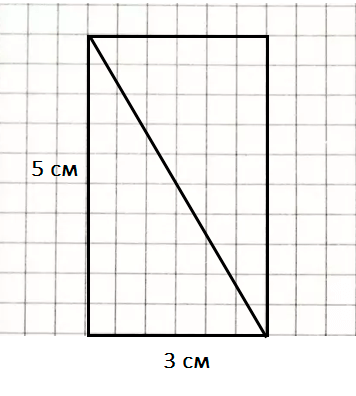
1) 5∙3=15 (см2 )=1500 (мм2)- площадь прямоугольника;
2) 1500÷2=750 (мм2)- площадь треугольника.
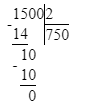
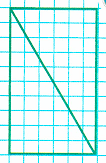

3) Найдем площадь одного треугольника:
1. Запишем длину прямоугольника:
3 см; – длина
2. Запишем ширину прямоугольника:
5 см; – ширина
3. Найдем площадь прямоугольника:
S = a · b = 3 · 5 = 15 см2; - площадь прямоугольника
4. Найдем площадь одного треугольника:
S = 15 см2 : 2 = 1 500 мм2 : 2 = 750 мм2; - площадь треугольника
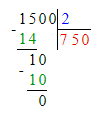
Краткое условие: За 7 дней израсходовали 21 кг масла. На сколько дней хватит 36 кг при той же норме? А если ежедневно расходовать на 1 кг больше?
За? дней израсходовали 36 кг масла;
Если каждый день на 1 кг больше-? дней 36 кг.
2) 36÷3=12 (дней)- израсходовали 36 кг масла;
3) 36÷(3+1)=9 (дней)- хватило бы 36 кг масла, если бы каждый день расходовали на 1 кг больше.
ШАГ 1. Найти сколько масла расходуется каждый день.
ШАГ 2. Найти на сколько дней хватит 36 кг масла.
ШАГ 3. Найти новый расход масла.
ШАГ 4. Найти на сколько дней хватит 36 кг масла при новом расходе.

1) 21 : 7 = 3 кг – за 1 день
Шаг 2. Найдем на сколько дней хватит 36 кг масла при таком расходе:
2) 36 : 3 = 12 дн. – при расходе 3 кг в день
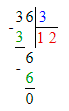
3) 3 + 1 = 4 кг – новый расход
Шаг 4. Найдем на сколько дней хватит 36 кг масла при новом расходе масла:
4) 36 : 4 = 9 дн. – при расходе 4 кг в день
2) 36 : 3 = 12 (дн.)
3) 3 + 1 = 4 (кг)
4) 36 : 4 = 9 (дн.)
Ответ: на 12 дней; на 9 дней.
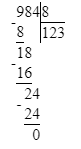
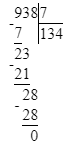
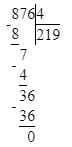
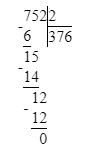
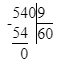
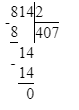
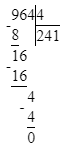
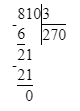



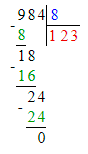
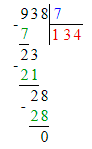
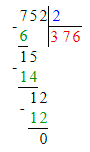
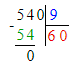




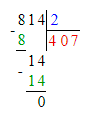
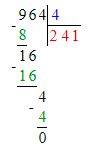

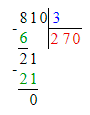

Краткое условие: Чем похожи и различаются уравнения и их решения в каждой паре?
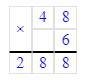
x+75=125∙3;x+75=375;x=375-75;x=300.
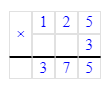
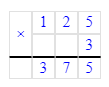
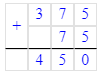
x∙10=250;x=250÷10;x=25.
x÷7=140;x=140∙7;x=980.
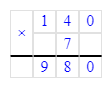
32÷x=32;x=32÷32;x=1.
1) х + 75 = 125 · 3;
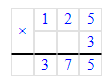
х = 375 - 75;
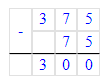
2) х - 75 = 125 · 3;
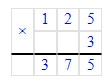
х = 375 + 75;
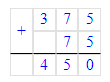
В первом уравнении неизвестно первое слагаемое, а во втором уравнении – уменьшаемое. Первое уравнение решается с помощью вычитания, а второе – с помощью сложения.
3) х · 10 = 250;
х = 250 : 10;
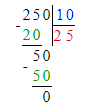
4) х : 10 = 250;
х = 250 · 10;
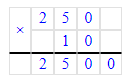
В первом уравнении неизвестен первый множитель, а во втором уравнении – делимое. Первое уравнение необходимо решать с помощью деления, а второе - с помощью умножения.
5) х : 7 = 140;
х = 140 · 7;
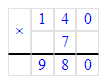
6) 140 : х = 7;
х = 140 : 7;
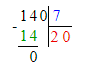
В первом уравнении неизвестно делимое, а во втором уравнении – делитель. Первое уравнение необходимо решать с помощью умножения, а второе - с помощью деления.
7) 32 : х = 32;
х = 32 : 32;
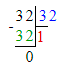
8) 32 · х = 32;
х = 32 : 32;
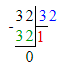
В первом уравнении неизвестен делитель, а во втором уравнении – второй множитель. Оба уравнения необходимо решать с помощью деления.
Краткое условие: На сколько равных частей разделён каждый квадрат? Найди площадь одной доли и сравни их.

1. Первый квадрат разделён на 4 равные части.
2. Второй квадрат разделён на 4 равные части.
3) Найдем площадь одной доли в каждом квадрате и сравним площади этих долей:
1. Длины сторон двух квадратов равны, значит, площади этих квадратов равны.
2. Сторона каждого квадрата равна 2 см.
3. Значит, площадь этих квадратов равняется:
S = а2 = 22 = 2 · 2 = 4 см2;
4. Так как площади двух квадратов равны и количество равных частей, на которые разделены квадраты также равны, значит, площади одной доли двух квадратов тоже равны.
5. S = 4 см2 : 4 = 1 см2;
Следовательно, площадь одной доли одного квадрата равняется площади одной доли второго квадрата и равняется 1 см2.

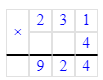
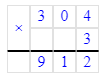
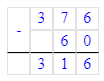
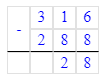
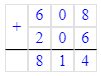
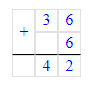
1. Сумма чисел 36 и 6 равняется 42. Следовательно, на месте сотен делимого нужно писать цифру 4, а на месте десятков – цифру 2.
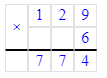
3. Подумаем, какое двузначное число делится на 9 без остатка при условии, что в этом числе 6 десятков. Частное чисел 63 и 9 равняется 7. Следовательно, в разряде единиц
делимого будет стоять число 3, а в разряде единиц частного – число 7.
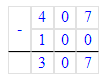
4. Значит, начальный ребус примет следующий вид:
423 : 9 = 47;
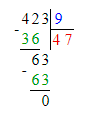
Страница 64. Номер: 295, 296, 297, 298, 299, задача на полях.



