ГДЗ 4 класс Математика Моро, Бантова, Бельтюкова

4класс

Страница 63, ГДЗ по математике за 4 класс к учебнику Моро часть 1

Выберите номер:

287 288 289 290 291 292 293 294 Задача на полях Ребус

Номер задания: 287

Краткое условие: Прочитай, как связаны числа при вычитании, и заполни таблицу.

Решение:

1) 42-36=6;
2) 45+85=130;
3) 60-28=32;
4) 537+362=899;

5) 846-140=706;

6) 542+834=1376.

Решение:

1) Запишем на с. 103, как связаны между собой числа при вычитании:
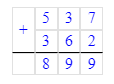
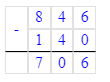
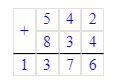
1. Если к разности прибавить вычитаемое, то получится уменьшаемое.
2. Если из уменьшаемого вычесть разность, то получится вычитаемое.
2) Рассмотрим таблицу:

3) Заполним таблицу:
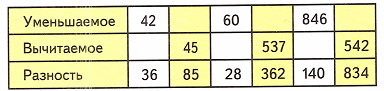
1. Чтобы найти вычитаемое, необходимо из уменьшаемого вычесть разность.
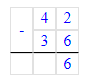
42 – 36 = 6;

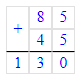
2. Чтобы найти уменьшаемое, необходимо к разности прибавить вычитаемое.
85 + 45 = 130;

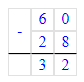
3. Чтобы найти вычитаемое, необходимо из уменьшаемого вычесть разность.
60 – 28 = 32;

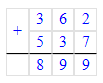
4. Чтобы найти уменьшаемое, необходимо к разности прибавить вычитаемое.
362 + 537 = 899;

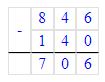
5. Чтобы найти вычитаемое, необходимо из уменьшаемого вычесть разность.
846 – 140 = 706;

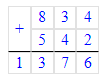
6. Чтобы найти уменьшаемое, необходимо к разности прибавить вычитаемое.
834 + 542 = 1 376;

Следовательно, начальная таблица примет следующий вид:

4) Рассмотрим решения уравнений:

5) Объясним решение уравнений и их проверку:
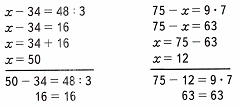
1. Для начала необходимо найти значение выражения справа. Частное чисел 48 и 3 равняется 16. Чтобы найти уменьшаемое, необходимо к разности прибавить вычитаемое. Сумма чисел 34 и 16 равна 50. При подстановке этого значения в начальное условие уравнения и решив его получится верное числовое равенство. Значит, уравнение решено верно.
2. Для начала необходимо найти значение выражения справа. Произведение чисел 9 и 7 равняется 63. Чтобы найти вычитаемое, необходимо из уменьшаемого вычесть разность. Разность чисел 75 и 63 равна 12. При подстановке этого значения в начальное условие уравнения и решив его получится верное числовое равенство. Значит, уравнение решено верно.

Номер задания: 288

Краткое условие: Реши уравнения.

Решение:

64-x=91÷7;64-x=13;x=64-13;x=51.

Ответ:

x=51.

Решение:

x-85=350+150;x-85=500;x=500+85;x=585.

Ответ:

x=585.

Решение:

Решим уравнения:
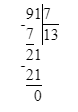
1) 64 - х = 91 : 7;

64 - х = 13;
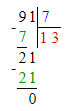
х = 64 – 13;

х = 51;
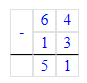
2) х - 85 = 350 + 150;

х - 85 = 500;
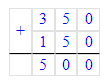
х = 500 + 85;

х = 585;

Ответ:

1) х = 51; 2) х = 585.

Номер задания: 289

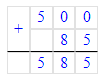
Краткое условие: Вычисли и сделай проверку.

Решение:

324 544+175 737=500 281;

Проверка:

840 103-62 524=777 579.

Проверка:

Решение:

Вычислим и сделаем проверку:
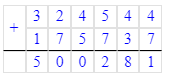
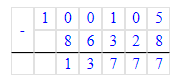
1) 324 544 + 175 737 = 500 281;

Проверка:
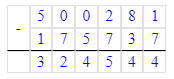
500 281 – 175 737 = 324 544;

324 544 = 324 544;
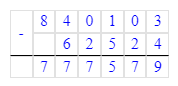
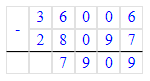
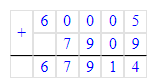
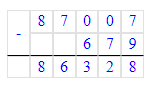
2) 840 103 – 62 524 = 777 579;

Проверка:
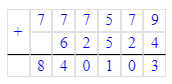
840 103 - 777 579 = 62 524;

62 524 = 62 524;

Ответ:

1) 500 281; 2) 777 579.

Номер задания: 290

Краткое условие: На полке лежат пакеты яблок массой 1 кг 200 г, 2 кг 100 г, 1 кг 900 г и 1 кг 700 г. Какие 2 пакета надо взять, чтобы их масса была меньше 3 кг?

Дано:

1 пакет - 1 кг 200 г;
2 пакет - 2 кг 100 г;
3 пакет - 1 кг 900 г;
4 пакет - 1 кг 700 г;

Решение:

Тогда:
Если взять 2 пакет и любой из трёх оставшихся, то их масса будет больше 3-х килограмм;
Значит, второй пакет с яблоками не рассматриваем.
1) 1 кг 200 г +1 кг 900 г=1200 г + 1900 г= 3 100 г > 3 кг- масса 1-го и 3-го пакетов больше 3 кг.
2) 1 кг 200 г + 1 кг 700 г =1 200 г + 1 700 г=2 кг 900 г < 3 кг- масса 1-го и 4-го пакетов меньше 3 кг.
3) 1 кг 900 г + 1 кг 700 г=1900 г+1700 г=3кг 600 г > 3 кг -
масса 3-го и 4-го пакетов больше 3 кг.
Таким образом, надо взять пакеты с яблоками массой 1 кг 200 г и 1 кг 700 г, чтобы их общая масса была меньше 3 кг.

Ответ:

1 кг 200 г и 1 кг 700 г.

Решение:

Подумаем, какие 2 пакета с яблоками надо взять, чтобы их масса была меньше трёх килограммов при условии, что масса пакетов равна: 1 кг 200 г; 2 кг 100 г; 1 кг 900 г; 1 кг 700 г.
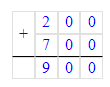
1) 1 кг 200 г + 2 кг 100 г = 3 кг 300 г;

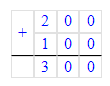
3 кг 300 г > 3 кг, что не удовлетворяет условию.
2) 2 кг 100 г + 1 кг 900 г = 3 кг 1 000 г = 4 кг;

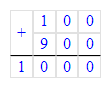
4 кг > 3 кг, что не удовлетворяет условию.
3) 1 кг 900 г + 1 кг 700 г = 2 кг 1 600 г = 3 кг 600 г;

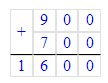
3 кг 600 г > 3 кг, что не удовлетворяет условию.
4) 1 кг 200 г + 1 кг 700 г = 2 кг 900 г;

2 кг 900 г < 3 кг, что удовлетворяет условию.
Следовательно, нужно взять первый и четвёртый пакет.

Ответ:

первый и четвёртый пакет.

Номер задания: 291

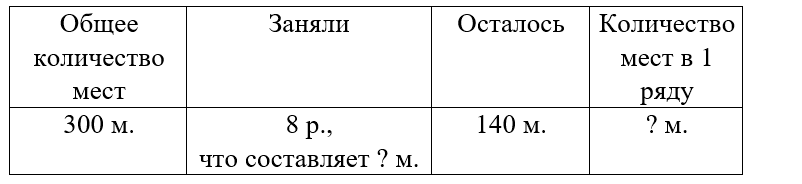
Краткое условие: В зале 300 мест. Когда заняли 8 рядов, осталось 140 мест. Сколько мест в каждом ряду?

Дано:

Всего – 300 мест;
Заняли - 8 рядов;
Осталось - 140 мест;
В 1 ряду - ? мест.

Решение:

1) 300-140=160 (мест)- заняли школьники;
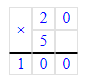
2) 160÷8=20 (мест)- в ряду.

Ответ:

20 мест в ряду.

Подсказка

Чтобы решить задачу, нужно:
ШАГ 1. Найти сколько мест заняли школьники.
ШАГ 2. Найти сколько мест в каждом ряду.

Дано:

Решение:

Шаг 1. Найдем сколько мест заняли:
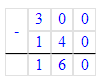
1) 300 - 140 = 160 м. – заняли

Шаг 2. Найдем сколько мест в каждом ряду:
2) 160 : 8 = 20 м. – в каждом ряду

Ответ:

в каждом ряду 20 мест.

Под запись в тетрадь:

1) 300 - 140 = 160 (м.)
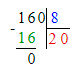
2) 160 : 8 = 20 (м.)
Ответ: в каждом ряду 20 мест.

Номер задания: 292

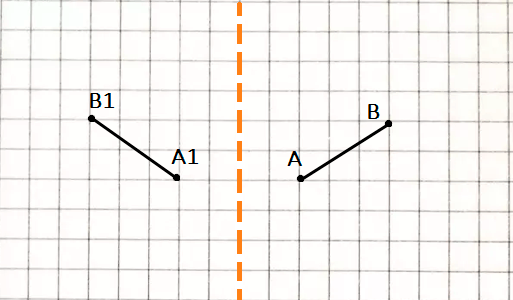
Краткое условие: 1) Чему равна треть отрезка 48 мм? 2) Начерти отрезок АВ и симметричный ему.

Дано:

Длина отрезка – 48 мм;
Третья часть - ? мм

Решение:

1) 48÷3=16 (мм)- третья часть отрезка длиной 48 мм.

Ответ:

16 мм.

Решение:

А1В1 симметричен АВ.

Решение:

1) Подумаем, чему равна третья часть отрезка длиной 48 мм: 48 мм : 3 = 16 мм;

Следовательно, третья часть отрезка длиной 48 мм равна 16 мм. 2) Рассмотрим отрезок АВ:

3) Начертим отрезок АВ:

4) Начертим отрезок ТМ, симметричный отрезку АВ:

Номер задания: 293

Решение:

1)
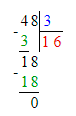
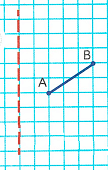
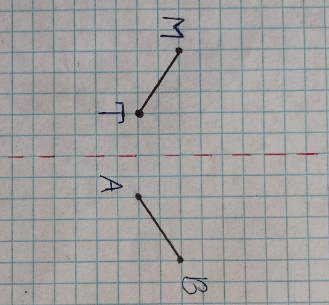
9 см=90 мм;
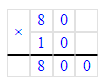
80 см=800 мм;
2 м 25 см=2 000 мм+250 мм=2 250 мм.
2)
9 ч=(9∙60) мин=540 мин;
180 с=(180÷60) мин=3 мин;
2 ч 25 мин=(2∙60) мин+25 мин=145 мин.

Решение:

Выразим:
1) в миллиметрах;
1. 9 см;
Так как 1 см = 10 мм, то 9 см = 9 · 10 мм = 90 мм;
2. 80 см;
Так как 1 см = 10 мм, то 80 см = 80 · 10 мм = 800 мм;

3. 2 м 25 см;
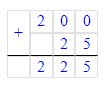
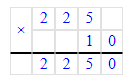
Так как 1 м = 100 см, а 1 см = 10 мм, то 2 м 25 см = 200 см + 25 см = 225 см = 225 · 10 мм = 2 250 мм;

2) в минутах;
1. 9 ч;
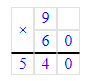
Так как 1 ч = 60 мин, то 9 ч = 9 · 60 мин = 540 мин;

2. 180 с;
Так как 1 мин = 60 с, то 180 с = 180 : 60 = 3 мин;

3. 2 ч 25 мин;
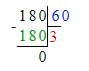
Так как 1 ч = 60 мин, то 2 ч 25 мин = 2 · 60 мин + 25 мин = 120 мин + 25 мин = 145 мин;

Ответ:

1) 90 мм; 800 мм; 2 250 мм; 2) 540 мин; 3 мин; 145 мин.

Номер задания: 294

Решение:

60 005 + (36 006 - 28 097)=67 914;

100 105 - (87 007 - 679)=13 777;

400 + 80 : 4 ∙ 5=500;

80÷4=20;

20∙5=100;

400+100=500.

800 - 640 : 2 : 4=720;

640÷2=320;

320÷4=80;

800-80=720.

Решение:

1) 60 005 + (36 006 - 28 097)=67 914;

2) 100 105 - (87 007 - 679)=13 777;

3) 400 + 80 : 4 ∙ 5=500;

4) 800 - 640 : 2 : 4=720;

Ответ:

1) 67 914; 2) 13 777; 3) 500; 4) 720.

Номер задания: Задача на полях

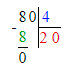
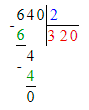
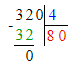
Краткое условие: Начерти отрезок, пятая часть которого равна 17 мм.

Решение:

1) Подумаем, чему равна длина отрезка, пятая часть которого равна 17 мм:
17 мм · 5 = 85 мм = 8 см 5 мм;

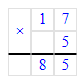
Следовательно, длина отрезка равна 8 см 5 мм.
2) Начертим отрезок АВ найденной длины:

Номер задания: Ребус

Решение:

1) Рассмотрим ребус:

2) Разгадаем ребус:
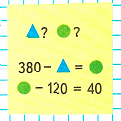
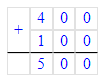
2) Узнаем, какие числа прячутся под треугольником и кругом:
1. Найдём, какое число прячется за кругом, решив второе выражение:
х - 120 = 40;
х = 40 + 120;

х = 160; - круг
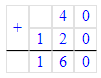
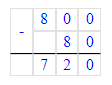
2. Найдём, какое число прячется за треугольником, решив первое выражение и подставив найденное значение:
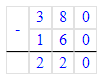
380 - х = 160;
х = 380 – 160;