ГДЗ 4 класс Математика Моро, Бантова, Бельтюкова

4класс

Страница 48, ГДЗ по математике за 4 класс к учебнику Моро часть 1

Выберите номер:

229 230 231 232 233 234 235 236 Задача на полях Задача на полях

Номер задания: 229

Краткое условие: В котором часу ты встаёшь? Когда ты идёшь в школу? В котором часу ложишься спать?

Решение:

Я встаю в 6 ч утра;
Иду в школу в 7 ч 50 мин. (уроки начинаются в 8 ч 30 мин);
Ложусь спать в 22 ч. (или в 10 ч. вечера).

Решение:

1) Запишем, в каком часу я встаю:
Я встаю в 7 : 00.
2) Запишем, в каком часу я иду в школу:
Я иду в школу в 8 : 20.
3) Запишем, в каком часу я ложусь спать:
Я ложусь спать в 21 : 15.

Номер задания: 230

Краткое условие: Сколько времени прошло от начала суток, если сейчас 2 ч ночи, 9 ч утра, 3 ч дня?

Решение:

Начало суток – 0 часов.
Если сейчас 2 ч. ночи, то от начала суток прошло 2 ч.
Если сейчас 9 ч. утра, то от начала суток прошло 9 ч.
Если сейчас 3 ч. дня (или 15 ч.), то от начала суток прошло 15 ч.

Решение:

1) Подумаем, сколько времени прошло от начала суток, если сейчас 2 ч ночи:
Если сейчас 2 ч ночи, то прошло: 0 + 2 = 2 ч;
2) Подумаем, сколько времени прошло от начала суток, если сейчас 9 ч утра:
Если сейчас 9 ч утра, то прошло: 0 + 9 = 9 ч;
3) Подумаем, сколько времени прошло от начала суток, если сейчас 3 ч дня:
Если сейчас 3 ч дня, то прошло: 0 + 12 + 3 = 15 ч;

Ответ:

2 часа; 9 часов; 15 часов.

Номер задания: 231

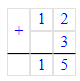
Краткое условие: Как сказать по-другому, сколько времени: 1) 16 ч, 20 ч, 21 ч 40 мин; 2) четверть пятого, половина первого, без четверти семь?

Решение:

1)
16 ч - это 4 ч дня;
20 ч – это 8 ч вечера;
21 ч 40 мин – это 9ч 40 мин вечера или без двадцати десять.
2)
Четверть пятого – это 4 ч 15 мин;
Половина первого – это 12 ч 30 мин;
Без четверти семь – это 6 ч 45 мин.

Решение:

Подумаем, как сказать по – другому, сколько сейчас времени:
1)
1. 16 ч;
(четыре часа дня);
2. 20 ч;
(восемь часов вечера);
3. 21 ч 40 мин;
(сорок минут десяти часов вечера);
2)
1. четверть пятого;
1) 04 : 15;
2) 16 : 15;
2. половина первого;
1) 00 : 30;
2) 12 : 30;
3. без четверти семь;
1) 06 : 45;
2) 18 : 45;

Номер задания: 232

Краткое условие: Вырази: 1) в часах: 2 сут, 10 сут 12 ч, 120 мин; 2) в сутках: 48 ч, 72 ч, 96 ч, 2 недели; 3) в месяцах: 3 года, 8 лет и 4 мес.; 4) в годах: 24 мес., 60 мес., 84 мес., 96 мес.

Решение:

1)
2 сут.=48 ч;
10 сут. 12 ч=(10∙24) ч+12 ч=240 ч+12 ч=252 ч;
120 мин=(120÷60) ч=2 ч;
2)
48ч=(48÷24) сут.=2 сут.;
72ч=(72÷24) сут.=3 сут.;
96ч=(96÷24) сут=4 сут.;
2 недели=(2∙7) дней=14 сут;
3)
3 года=(3∙12) мес.=36 мес.;
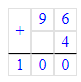
8 лет и 4 месяца=(8∙12) мес.+4 мес.=100 мес.;
4)
24 мес.=(24÷12) лет=2года;
60 мес.=(60÷12) лет=5 лет;
84 мес.=(84÷12) лет=7 лет;
96 мес.=(96÷12) лет=8 лет.

Решение:

Выразим:
1) в часах;
1. 2 сут.;
Так как 1 сут. = 24 ч, то 2 сут. = 2 · 24 ч = 48 ч;

2. 10 сут. 12 ч;
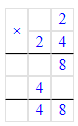
Так как 1 сут. = 24 ч, то 10 сут. 12 ч = 10 · 24 ч + 12 ч = 240 ч + 12 ч = 252 ч;

3. 120 мин;
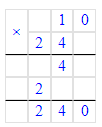
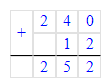
Так как 1 ч = 60 мин, то 120 мин = 120 мин : 60 мин = 2 ч;

2) в сутках;
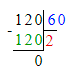
1. 48 ч;
Так как 1 сут. = 24 ч, то 48 ч = 48 ч : 24 ч = 2 сут.;

2. 72 ч;
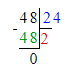
Так как 1 сут. = 24 ч, то 72 ч = 72 ч : 24 ч = 3 сут.;

3. 96 ч;
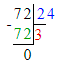
Так как 1 сут. = 24 ч, то 96 ч = 96 ч : 24 ч = 4 сут.;

4. 2 недели;
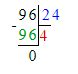
Так как 1 неделя = 7 сут., то 2 недели = 2 · 7 сут. = 14 сут.;
3) в месяцах;
1. 3 года;
Так как 1 год = 12 мес., то 3 года = 3 · 12 = 36 мес.;

2. 8 лет и 4 мес.;
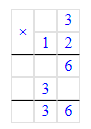
Так как 1 год = 12 мес., то 8 лет и 4 мес. = 8 · 12 + 4 = 96 + 4 = 100 мес.;

4) в годах;
1. 24 мес.;
Так как 1 год = 12 мес., то 24 мес. = 24 : 12 = 2 года;

2. 60 мес.;
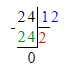
Так как 1 год = 12 мес., то 60 мес. = 60 : 12 = 5 лет;

3. 84 мес.;
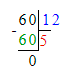
Так как 1 год = 12 мес., то 84 мес. = 84 : 12 = 7 лет;

4. 96 мес.;
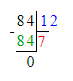
Так как 1 год = 12 мес., то 96 мес. = 96 : 12 = 8 лет;

Ответ:

1) 48 ч; 252 ч; 2 ч; 2) 2 сут.; 3 сут.; 4 сут.; 14 сут.; 3) 36 мес.; 100 мес.; 4) 2 года; 5 лет; 7 лет; 8 лет.

Номер задания: 233

Краткое условие: Чем похожи и различаются уравнения каждой пары? Чем похожи и различаются их решения?

Решение:

Уравнения первой пары похожи тем, что неизвестен один из множителей, а число произведения равно 45 000; различаются числом второго множителя.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель; тогда их решения похожи, но отличаются ответы.
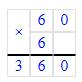
x∙10=45 000;x=45 000÷10;x=4 500.
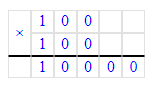
100∙x=45 000;x=45 000÷100;x=450.
Уравнения второй пары похожи данными числами, а отличаются неизвестными.
В первом уравнении надо найти делимое: для этого частное умножаем на делитель;
А во втором уравнении надо найти делитель: для этого делимое делим на частное.
x÷100=4 000;x=4000∙100;x=400 000.
4 000÷x=100;x=4 000÷100;x=40.
Уравнения третьей пары похожи данными числами, а отличаются действиями.
В первом уравнении надо найти первое слагаемое:
для этого из суммы вычитаем второе слагаемое;
а во втором уравнении надо найти уменьшаемое: для этого к разности прибавляем вычитаемое.
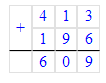
x+190=400;x=400-190;x=210.
x-190=400;x=400+190;x=590.

Решение:

Сравним уравнения каждой пары и их решения:
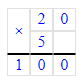
1) х · 10 = 45 000;
х = 45 000 : 10;

х = 4 500;
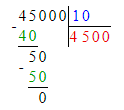
2) 100 · х = 45 000;
х = 45 000 : 100;

х = 450;
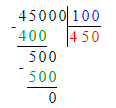
В первом уравнении неизвестен первый множитель, а во втором уравнении – второй множитель. Оба уравнения решаются с помощью деления.
3) х : 100 = 4 000;
х = 4 000 · 100;

х = 400 000;
4) 4 000 : х = 100;
х = 4 000 : 100;

х = 40;
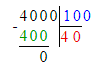
В первом уравнении неизвестно делимое, а во втором уравнении – делитель. Первое уравнение необходимо решать с помощью умножения, а второе - с помощью деления.
5) х + 190 = 400;
х = 400 - 190;

х = 210;
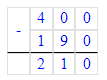
6) х - 190 = 400;
х = 400 + 190;

х = 590;
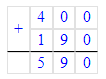
В первом уравнении неизвестно первое слагаемое, а во втором уравнении – уменьшаемое. Первое уравнение необходимо решать с помощью вычитания, а второе - с помощью сложения.

Номер задания: 234

Краткое условие: Из 1 ц свежих яблок получилось 16 кг сушёных. На сколько килограммов масса сушёных яблок меньше массы свежих?

Дано:

1 ц свежих яблок – 16 кг сушёных;
На сколько кг масса сушёных яблок меньше массы свежих?

Решение:

1) 1ц=100 кг; 100-16=на 84 (кг)- масса сушёных яблок меньше массы свежих.

Ответ:

на 84 кг.

Подсказка

Чтобы решить задачу, нужно:
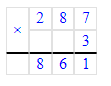
ШАГ 1. Найти массу свежих яблок в килограммах.
ШАГ 2. Найти на сколько килограммов масса сушёных яблок меньше массы свежих яблок.

Дано:

Решение:

Шаг 1. Найдем массу свежих яблок в килограммах:
1) 1 ц = 100 кг – свежие яблоки
Шаг 2. Найдём на сколько килограммов масса сушёных яблок меньше массы свежих:
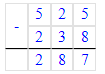
2) 100 - 16 = 84 кг – на столько меньше

Ответ:

сушёных яблок на 84 кг меньше.

Под запись в тетрадь:

1) 1 ц = 100 кг
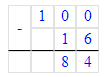
2) 100 - 16 = 84 (кг)
Ответ: сушёных яблок на 84 кг меньше.

Номер задания: 235

Краткое условие: Масса масла в бутылке 500 г. Сколько масла в 10 бутылках?

Дано:

Масса бутылки с маслом -600 г;
Масса пустой бутылки – 100 г;
В 10 бутылок -? масла.

Решение:

1) 600-100=500 (г)- масса масла в 1-й бутылке;
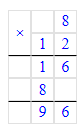
2) 500∙10=5 000 (г)=5 (кг)- масла можно налить в 10 таких бутылок.

Ответ:

5 кг.

Подсказка

Чтобы решить задачу, нужно:
ШАГ 1. Найти массу масла в одной бутылке.
ШАГ 2. Найти сколько масла можно налить в 10 бутылок.

Дано:

Решение:

Шаг 1. Найдем массу масла в 1 бутылке:
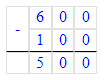
1) 600 - 100 = 500 г – масса масла в 1 бутылке

Шаг 2. Найдём сколько масла можно налить в 10 бутылок:
2) 500 · 10 = 5 000 г = 5 кг – масса масла в 10 бутылках

Ответ:

в 10 бутылок можно налить 5 кг масла.

Под запись в тетрадь:

1) 600 - 100 = 500 (г)
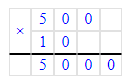
2) 500 · 10 = 5 000 (г) = 5 (кг)
Ответ: в 10 бутылок можно налить 5 кг масла.

Номер задания: 236

Решение:

6 000 : (20 ∙ 5) ∙ 6=360;

20∙5=100;

6 000÷100=60;

60∙6=360.

1 000 : (90 : 9) ∙ 100=10 000;

90÷9=10;

1 000÷10=100;

100∙100=10 000.

(525 - 238) ∙ 3=861;

(517 - 450) ∙ 9=603;

(924 - 207) : 3=239;

(413 + 196) : 7=87.

Решение:

1) 6 000 : (20 ∙ 5) ∙ 6=360;

2) 1 000 : (90 : 9) ∙ 100=10 000;

3) (525 - 238) ∙ 3=861;

4) (517 - 450) ∙ 9=603;

5) (924 - 207) : 3=239;

6) (413 + 196) : 7=87.

Ответ:

1) 360; 2) 10 000; 3) 861; 4) 603; 5) 239; 6) 87.

Номер задания: Задача на полях

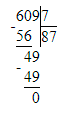
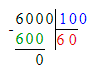
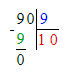
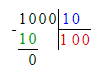
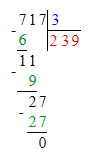
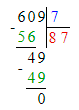
Краткое условие: Какое время показывают электронные часы? Какое это время суток?

Решение:

1) Рассмотрим рисунок:

2) Подумаем, какое время показывают часы:
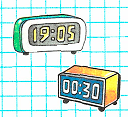
1. Первые часы показывают пять минут восьмого.
2. Вторые часы показывают половину первого.
3) Подумаем, какое время суток показывают часы:
1. Первые часы показывают вечернее время суток.
2. Вторые часы показывают ночное время суток.

Номер задания: Задача на полях

Решение:

1) Рассмотрим рисунок:

2) Скажем, какое время показывают каждые часы:
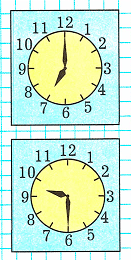
1. Первые часы показывают семь часов утра или семь часов вечера.
2. Вторые часы показывают половину десятого часа дня или половину десятого вечера.

Страница 47 Страница 49