Страница 42, ГДЗ по математике за 4 класс к учебнику Моро часть 1
Страница 42
Краткое условие: 1) В магазин привезли 48 коробок винограда: 16 коробок чёрного по 9 кг, остальные — зелёный по 8 кг. Сколько всего килограммов винограда привезли? 2) В магазин привезли 400 кг винограда: несколько коробок чёрного по 9 кг и 32 коробки зелёного по 8 кг. Сколько коробок чёрного винограда привезли?

3) 8∙32=256 (кг)- зелёного винограда привезли в магазин;

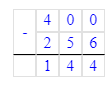
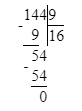
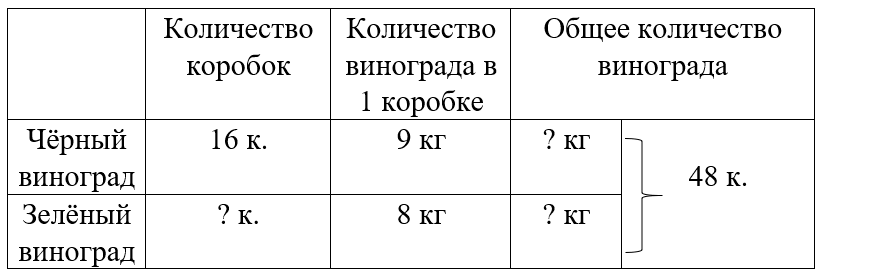
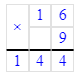
1) 16 · 9 = 144 кг – чёрный виноград

2) 48 - 16 = 32 к. – с зелёным виноградом
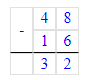
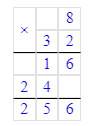
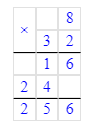
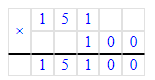
3) 32 · 8 = 256 кг – зелёный виноград

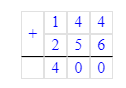
4) 256 + 144 = 400 кг – всего

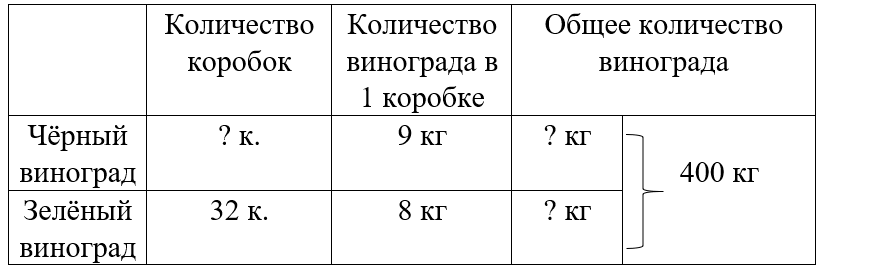
1) 32 · 8 = 256 кг – зелёный виноград

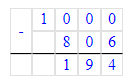
2) 400 - 256 = 144 кг – чёрный виноград

3) 144 : 9 = 16 к. – с чёрным виноградом
Краткое условие: Робот-пылесос убирает 50 м² на одной зарядке. Сколько зарядок нужно для уборки 120 м²?
120 м2-? зарядок.
ШАГ 1. Найти сколько раз нужно зарядить робот - пылесос.

1) 120 : 50 = 2 (ост. 20) – значит, 2 зарядок не хватит
Ответ: 3 зарядки.
Краткое условие: Чем похожи и различаются уравнения в парах? В каком уравнении неизвестное больше? Сделай вывод и проверь решением.
Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое; тогда, неизвестное число больше во 2-м уравнении.
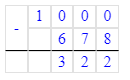
х+37=78; х=78-37; х=41.
х+37=80; х=80-37; х=43.
Уравнения второй пары похожи тем, что неизвестно вычитаемое, а уменьшаемое равно 90; различаются числом разности.
Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность; тогда, неизвестное число больше в первом уравнении.
90-х=47; х=90-47; х=43.
90-х=50; х=90-50; х=40.
Уравнения третьей пары похожи тем, что неизвестно уменьшаемое, а вычитаемое равно 28; различаются числом разности.
Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое; тогда, неизвестное число больше в первом уравнении.
х-28=32; х=32+28; х=60. х-28=22; х=22+28; х=50.
Уравнения четвёртой пары похожи тем, что неизвестно второе слагаемое, а первое слагаемое равно 45; различаются числом суммы.
Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое; тогда, неизвестное число больше во 2-м уравнении.
45+х=63; х=63-45; х=18.
45+х=68; х=68-45; х=23.
1) х + 37 = 78;
х = 78 – 37;
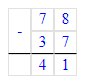
2) х + 37 = 80;
х = 80 – 37;
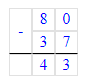
Так как 43 > 41 и сравнивая первый столбик уравнений можно сделать вывод, что неизвестное число второго уравнения больше.
3) 90 - х = 47;
х = 90 – 47;
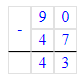
4) 90 - х = 50;
х = 90 – 50;
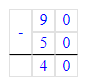
Так как 43 > 40 и сравнивая второй столбик уравнений можно сделать вывод, что неизвестное число первого уравнения больше.
5) х - 28 = 32;
х = 32 + 28;
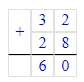
6) х - 28 = 22;
х = 22 + 28;
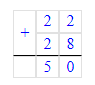
Так как 60 > 50 и сравнивая третий столбик уравнений можно сделать вывод, что неизвестное число первого уравнения больше.
7) 45 + х = 63;
х = 63 - 45;
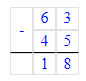
8) 45 + х = 68;
х = 68 - 45;
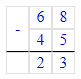
Так как 23 > 18 и сравнивая четвёртый столбик уравнений можно сделать вывод, что неизвестное число второго уравнения больше.
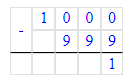
1 000 000÷1 000-999=1 000-999=1;
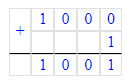
1 000 000÷1 000+1=1000+1=1 001;
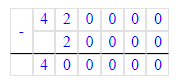
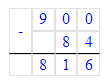
420 000-20 000=400 000;
28 000÷4∙100=7 000∙100=700 000.
2)
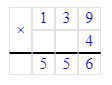
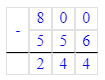
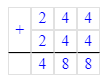
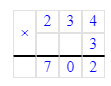
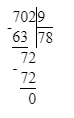
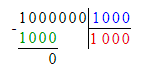
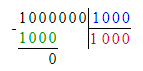






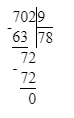

Тогда:
5∙5=25;
25∙2=50;
50+14=64;
64-8=56 (отбросим цифру 5);
6∙7=42;
42÷2=21.
Пусть задуманное число равно 2.
Тогда:
2∙5=10;
10∙2=20;
20+14=34;
34-8=26 (отбросим цифру 2);
6∙7=42;
42÷2=21.
В результате всегда будет 21, потому что при умножении любого числа на 5, а затем на 2 полученное число будет оканчиваться на нуль;
Если к числу, которое оканчивается на нуль, прибавить 14 и вычесть 8 (т.е. прибавить 6), то оно будет оканчиваться на 6;
Так как после 4-го действия 1-я цифра результата отбрасывается, то в итоге всегда остаётся число 6;
При умножении числа 6 на 7 будет 42, а при делении числа 42 на 2 будет 21.
Предположим, задумали число 9.
2) Умножим его на 5;
9 · 5 = 45;
3) Произведение увеличим в 2 раза;
45 · 2 = 90;
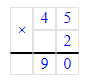
90 + 14 = 104;
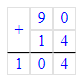
104 – 8 = 96;
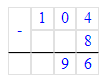
Если от числа 96 отбросить слева первую цифру, то получится 6;
7) Оставшееся число умножим на 7 и разделим на 2;
6 · 7 : 2 = 42 : 2 = 21;
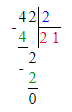
Так как любое число умножается на 5, а далее на 2, то в итоге задуманное число умножается на 10. Соответственно, если на 10 умножается однозначное число, то в результате получается двузначное число, которое оканчивается на нуль. Далее к полученному результату прибавляется число 14 и вычитается число 8, следовательно, к числу прибавляется число 6. В итоге мы к двузначному числу, кратному 10 прибавляем 6 и получаем двузначное число, которое оканчивается на 6, а когда мы уберем одну цифру слева, то останется число 6. Далее число 6 умножается на 7 и делится на 2, получая 21.
1) определить, записанное число меньше или больше 100;
2) если меньше 100, то умножить это число на 6 и вывести полученное число;
3) если больше 100, то сразу вывести это число.
Если на входе число 7, то на выходе 42:
7<100- да;
7∙6=42.
Если на входе число 8, то на выходе 48:
8<100- да;
8∙6=48.
Если на входе число 10, то на выходе 60:
10<100 - да;
10∙6=60.
Если на входе число 200, то на выходе будет само это число:
200<100 - нет.
Если на входе число 12, то на выходе 72:
12<100- да;
12∙6=72.
Если на входе число 158, то на выходе будет само это число:
158<100- нет.
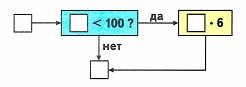
1. Задаётся произвольное число.
2. Число сравнивается с числом 100.
3. Если число больше ста, число подается на выход машины.
4. Если число меньше ста, оно умножается на 6 и подается на выход машины.
3) Подумаем, какое число будет получаться на выходе из машины, если на входе будут числа:
1) 7;
7 < 100;
7 · 6 = 42;
Следовательно, на выходе будет число 42.
2) 8;
8 < 100;
8 · 6 = 48;
Следовательно, на выходе будет число 48.
3) 10;
10 < 100;
10 · 6 = 60;
Следовательно, на выходе будет число 60.
4) 200;
200 > 100;
Следовательно, на выходе будет число 200.
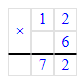
5) 12;
12 < 100;
12 · 6 = 72;
6) 158;
158 > 100;
Следовательно, на выходе будет число 158.
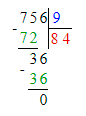
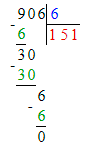
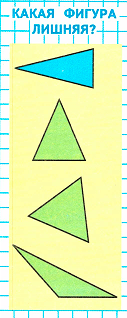
2. Лишним может быть четвёртый треугольник, так как он является тупоугольным, а все остальные – остроугольные.
3. Лишним может быть третий треугольник, так как он является равносторонним, а все остальные не являются равносторонними.
Страница 42. Номер: 191, 192, 193, 194, 195, 196, задача на полях.



