Страница 38, ГДЗ по математике за 4 класс к учебнику Моро часть 1
Страница 38
2) Ширина стола – 6 дм.
3) Расстояние от города до посёлка – 18 км.
4) Высота телеграфного столба – 6 м.
5) Толщина книги – 20 мм.
1) Длина карандаша – 18 см;
2) Ширина стола – 6 дм;
3) Расстояние от города до посёлка – 18 км;
4) Высота телефонного столба – 6 м;
5) Толщина книги – 20 мм;
Краткое условие: Орлы поднимаются до 3 000 м, журавли — до 4 000 м. Вырази высоту в километрах.
Орлы: 3 000 м = 3 км.
Журавли: 4 000 м = 4 км.
Так как 1 км = 1 000 м, то:
3 000 м = 3 км;
4 000 м = 4 км;
Следовательно, орлы поднимаются на высоту до 3 км, а журавли – до 4 км.
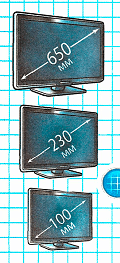
Краткое условие: Размеры экранов телевизоров указаны в миллиметрах. Вырази их в сантиметрах.
650 мм = 65 см;
230 мм = 23 см;
100 мм = 10 см.
Так как 1 см = 10 мм, то:
1. 650 мм = 65 см;
2. 230 мм = 23 см;
3. 100 мм = 10 см;
Краткое условие: Спортсменка прыгнула на 2 м Об см, спортсмен — на 2 м 41 см. Вырази высоту в сантиметрах.
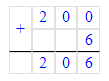
2 м 06 см=200 см+6 см = 206 см;
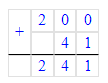
2 м 41 см= 200 см+41 см = 241 см.
Так как 1 м = 100 мм, то:
2 м 06 см = 200 см + 6 см = 206 см;
365 ед. = 36 дес. 5 ед.;
2 120 ед. = 21 сот. 2 дес.;
5 050 ед. = 5 тыс. 50 ед;
100 мм = 10 см;
184 дм = 18 м 4 дм;
1 190 см = 11 м 9 дм;
9 006 м = 9 км 6 м.
2) 365 ед. = 36 дес. 5 ед.;
3) 2 120 ед. = 21 сот. 2 дес.;
4) 5 050 ед. = 5 тыс. 50 ед.;
5) 100 мм = 10 см;
6) 184 дм = 18 м 4 дм;
7) 1 190 см = 11 м 9 дм;
8) 9 006 м = 9 км 6 м;
Краткое условие: Выполни деление с остатком и сделай проверку.
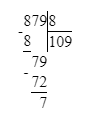
1) 7<8
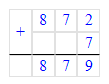
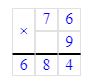
2) 109∙8=872
3) 872+7=979.
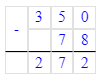
791÷9=87(ост.8);
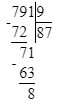
1) 8<9
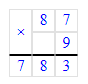
2) 87∙9=783
3) 783+8=791.
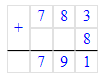
677÷7=96(ост.5);
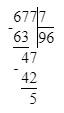
1) 5<7
2) 96∙7=672
3) 672+5=677.
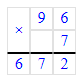
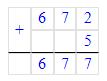
960÷9=106(ост.6).
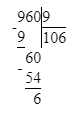
1) 6<9
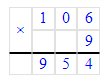
2) 106∙9=954
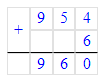
3) 954+6=960.
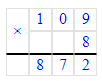
1) 879÷8=109(ост.7);
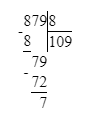
1) 7<8
2) 109∙8=872
2) 791÷9=87(ост.8);
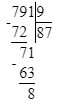
1) 8<9
2) 87∙9=783
3) 677÷7=96(ост.5);
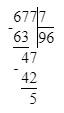
1) 5<7
2) 96∙7=672
4) 960÷9=106(ост.6).
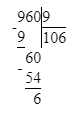
1) 6<9
2) 106∙9=954
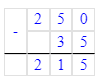
Краткое условие: Из двух городов, расстояние между которыми 650 км, вышли навстречу два поезда; один прошёл 250 км, другой — на 35 км меньше. На каком расстоянии поезда друг от друга?
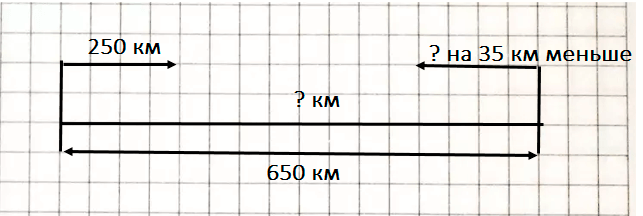
ШАГ 1. Найти расстояние второго поезда.
ШАГ 2. Найти пройденное расстояние двух поездов.
ШАГ 3. Найти на каком расстоянии друг от друга находятся поезда.

1) 250 - 35 = 215 км – расстояние второго поезда

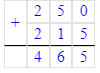
2) 250 + 215 = 465 км – расстояние двух поездов

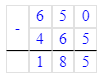
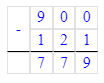
3) 650 - 465 = 185 км – расстояние между двумя поездами

2) 250 + 215 = 465 (км)
3) 650 - 465 = 185 (км)
Ответ: расстояние между двумя поездами равняется 185 км.
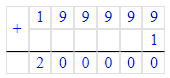
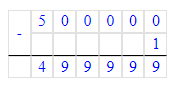
500 000-1=499 999;
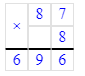
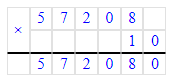
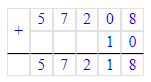
57 208∙10=572 080;
57 208+10=57 218;
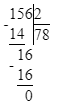
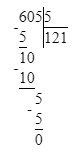
ШАГ 1. Выполняем действия в скобках.
ШАГ 2. Выполняем умножение и деление по порядку.
ШАГ 3. Выполняем сложение и вычитание по порядку.
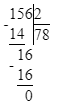

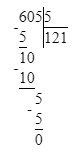



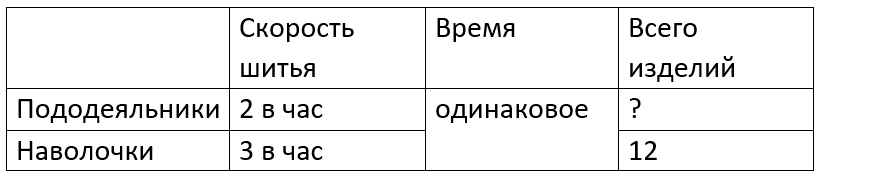
Краткое условие: Две швеи работали одинаковое время. Первая сшила 12 наволочек по 3 в час. Сколько пододеяльников сшила вторая, если она шила по 2 в час?
2) 2∙4=8 (пододеяльников)- сшила вторая швея.
ШАГ 1. Найти время работы двух швей.
ШАГ 2. Найти количество сшитых пододеяльников.
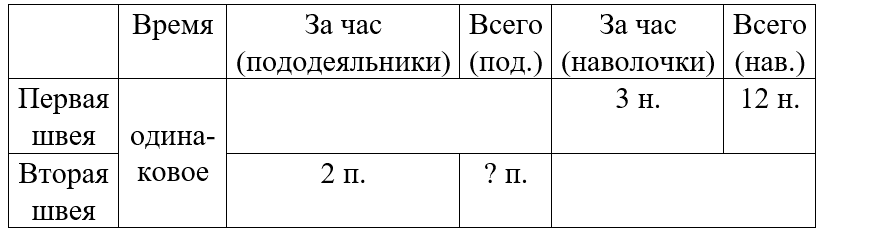
1) 12 : 3 = 4 ч – время работы
Шаг 2. Найдём сколько пододеяльников сшила вторая швея:
2) 2 · 4 = 8 п. – сшила вторая швея
2) 2 · 4 = 8 (п.)
Ответ: вторая швея сшила 8 пододеяльников.
Краткое условие: Назови прямые, тупые, острые углы, виды треугольников и число осей симметрии фигуры ABCD.
Тупые углы: ABC. BCD.
Острые углы: DAB, ADB, ABD, DBC, BDC.
Треугольники:
ABC - остроугольный равносторонний;
BCD - тупоугольный равнобедренный.
У фигуры ABCD одна ось симметрии, проходящая через отрезок АС.
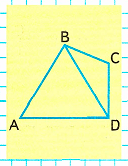
Прямые углы: ∠ADC;
Тупые углы: ∠BCD; ∠ABC;
Острые углы: ∠ABD; ∠BAD; ∠BDA; ∠CBD; ∠BCD;
3) Назовём виды треугольников:
ΔABD – равносторонний;
ΔBCD – равнобедренный;
4) Подумаем, сколько осей симметрии у фигуры ABСD:
У данной фигуры 1 ось симметрии.
Краткое условие: Самая длинная дистанция в соревнованиях по бегу 42 195 м. Сколько это километров и метров?
Так как 1 км = 1 000 м, то:
42 195 м = 42 км 195 м;
Страница 38. Номер: 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, задача на полях.



