Страница 35, ГДЗ по математике за 4 класс к учебнику Моро часть 1
Страница 35
Краткое условие: Выполни деление с остатком и сделай проверку.
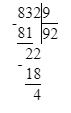
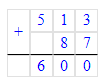
1) 4<9
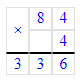
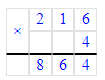
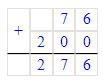
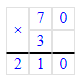
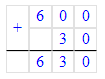
2) 92∙9=828
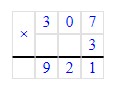
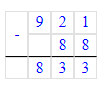
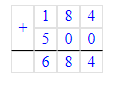
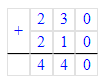
3) 828+4=832.
641÷3=213 (ост.2)
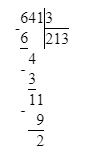
1) 2<3
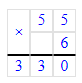
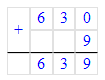
2) 213∙3=639
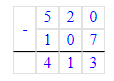
3) 639+2=641.
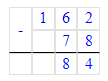
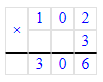
587÷8=73 (ост.3);
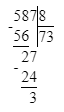
1) 3<8
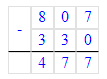
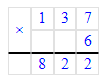
2) 73∙8=584
3) 584+3=587.
667÷7=95 (ост.2).
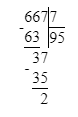
1) 2<7
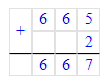
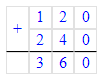
2) 95∙7=665
3) 665+2=667.
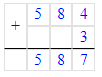
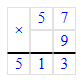
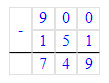
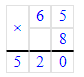
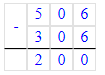
1) 832÷9=92 (ост.4);
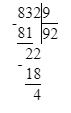
1) 4<9
2) 92∙9=828
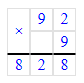
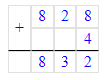
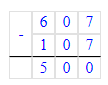
2) 641÷3=213 (ост.2)
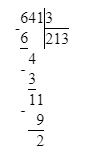
1) 2<3
2) 213∙3=639
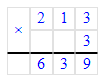
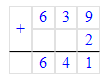
3) 587÷8=73 (ост.3);
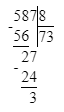
1) 3<8
2) 73∙8=584
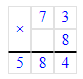
4) 667÷7=95 (ост.2).
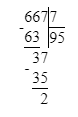
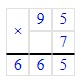
1) 2<7
2) 95∙7=665
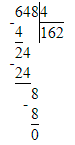
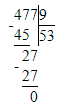
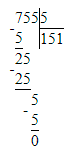
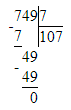
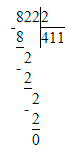
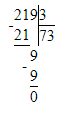


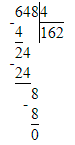




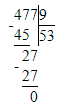
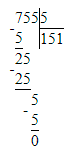

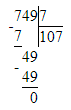

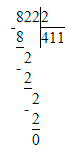
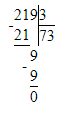

Краткое условие: Реши уравнения.
Ответ: x=1.
x-12=0; x=12.
Ответ: x=12.
32÷x=1;x=32÷1;x=32.
Ответ: x=32.
83-x=0;x=83.
Ответ: x=83.
1) 7 · х = 7;
х = 7 : 7;
х = 1;
2) х – 12 = 0;
х = 12 + 0;
х = 12;
3) 32 : х = 1;
х = 32 : 1;
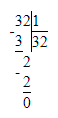
4) 83 – х = 0;
х = 83 - 0;
х = 83;
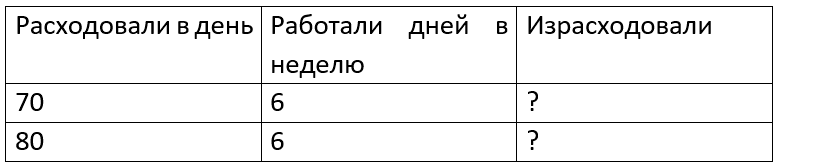
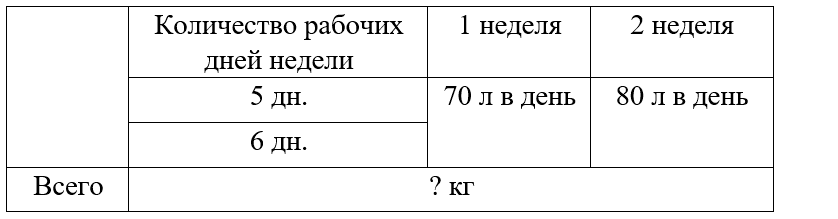
Краткое условие: 1) В магазин привезли 5 контейнеров мандаринов по 40 кг и 5 контейнеров винограда по 35 кг. Продали 120 кг мандаринов и 140 кг винограда. Сколько килограммов фруктов осталось? 2) Столовая расходовала одну неделю по 70 л молока в день, другую — по 80 л. Сколько литров молока израсходовали за две недели, если столовая работала 5 дней в неделю? 6 дней?
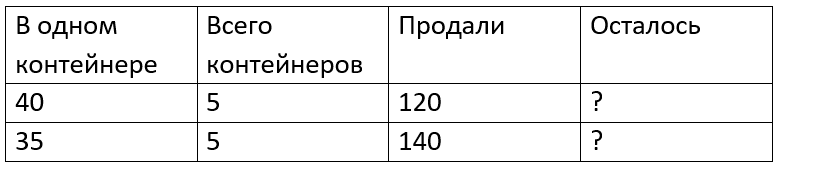
2) 35∙5=175 (кг)- винограда привезли всего;
3) 200-120=80 (кг)-мандаринов осталось продать;
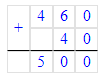
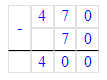
4) 175-140=35 (кг)- винограда осталось продать;
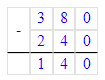
5) 80+35=115 (кг)- мандаринов и винограда осталось продать.

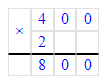
2) 80∙5=400 (л)- молока израсходовали во 2-ю неделю;
3) 350+400=750 (л)- молока израсходовали за 2 недели.
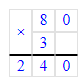
2) 150∙6=900 (л)- молока израсходовали за эти две недели.
1)

Шаг 1. Найдём сколько было килограммов риса:
1) 5 · 40 = 200 кг – было риса
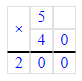
2) 5 · 35 = 175 кг – было пшена

3) 200 + 175 = 375 кг – было крупы
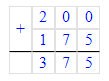
4) 120 + 140 = 260 кг – продали
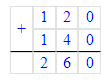
5) 375 - 260 = 115 кг – осталось продать
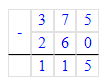
Шаг 1. Найдём сколько было килограммов риса:
1) 5 · 40 = 200 кг – было риса
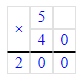
2) 200 - 120 = 80 кг – осталось риса
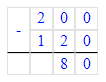
3) 5 · 35 = 175 кг – было пшена

4) 175 - 140 = 35 кг – осталось пшена
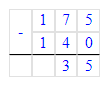
5) 80 + 35 = 115 кг – осталось продать
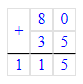
Шаг 1. Найдём сколько молока израсходовали за 1 неделю из 5 рабочих дней:
1) 70 · 5 = 350 л – за 1 неделю из 5 дней
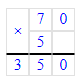
2) 80 · 5 = 400 л – за 2 неделю из 5 дней
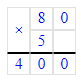
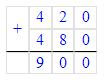
3) 350 + 400 = 750 л – всего
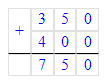
4) 70 · 6 = 420 л – за 1 неделю из 6 дней
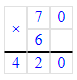
5) 80 · 6 = 480 л – за 2 неделю из 6 дней
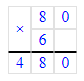
6) 420 + 480 = 900 л – всего
Шаг 1. Найдём сколько молока израсходовали за 2 дня на первой и второй неделе вместе:
1) 70 + 80 = 150 л – за 2 дня на двух неделях
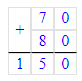
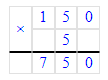
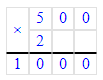
2) 150 · 5 = 750 л – всего
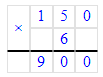
3) 150 · 6 = 900 л – всего
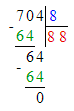
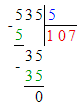
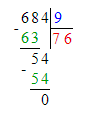
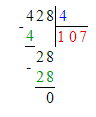
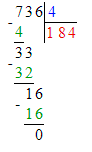



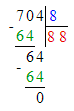


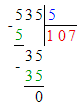



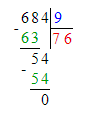
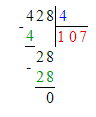

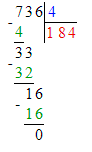

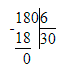
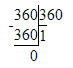

Краткое условие: Сколько разрядов в классе? Назови разряды и классы.
Классы называются: единицы, тысячи, миллионы, миллиарды.
В каждом классе содержится по 3 разряда.
2) Подумаем, как называются разряды и классы:
Классы: класс единиц, класс тысяч, класс миллионов, класс миллиардов.
В каждом классе имеются следующие разряды: единицы, десятки, сотен.
Краткое условие: Покажи на примере, что 10 единиц одного разряда — это единица следующего.
10 дес.=1 сот.
10 сот.= 1 тыс.
10 тыс.=1 дес. тыс.
Таким образом, 10 единиц любого разряда образуют единицу следующего разряда.
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 10;
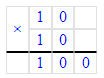
10 единиц – это 1 десяток;
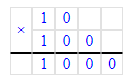
10 десятков – это 1 сотня, так как 10 · 10 = 100;
Краткое условие: Покажи на примере, что 1000 единиц одного класса образуют единицу следующего.
1 000 ед. класса тысяч= 1 ед. класса миллионов.
1 000 ед. класса миллионов= 1 ед. класса миллиардов.
Таким образом, 1 000 единиц одного класса образуют единицу следующего класса.
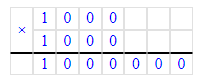
1 000 единиц – это 1 тысяча;
1 000 тысяч – это 1 миллион, так как 1 000 · 1 000 = 1 000 000;
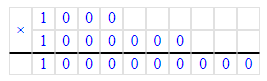
Краткое условие: Сколько цифр используется для записи чисел? Назови их и покажи, как одними цифрами записать разные числа.
0,1,2,3,4,5,6,7,8,9.
Например, возьмём 3 цифры: 3,4,5;
Запишем разные числа:
345,354,534,543,435,453.
Этот пример показывает, что одними и теми же цифрами можно записать разные числа.
Для записи цифр используется 10 чисел.
2) Назовём эти числа:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9;
3) Покажем, как можно одними и теми же цифрами записать разные числа:
Для примера возьмём цифры 2, 6, 9. С помощью этих цифр можно записать следующие числа:
962; 692; 269; 296; 629; 926.
Краткое условие: Покажи на примере, как меняется значение цифры при изменении её позиции в числе.
Число 256 - цифра 2 обозначает сотни;
Число 526 - цифра 2 обозначает десятки;
Число 652 - цифра 2 обозначает единицы.
Данный пример показывает, как изменяется значение цифры при изменении её места в записи числа.
Для примера возьмём цифры числа 146 и 416.
В числе 146 одна сотня, четыре десятка и шесть единиц. Цифры 1 и 4 поменяли местами. Следовательно, получили число 416, в котором четыре сотни, один десяток и шесть единиц. Соответственно, при изменении места цифры в записи числа меняется её разряд.
Краткое условие: Как увеличить число в 10, 100, 1 000 раз?
Чтобы получить число, которое больше данного в 10 раз, необходимо начальное число умножить на 10.
2) Подумаем, как получить число, которое больше данного в 100 раз:
Чтобы получить число, которое больше данного в 100 раз, необходимо начальное число умножить на 100.
3) Подумаем, как получить число, которое больше данного в 1 000 раз:
Чтобы получить число, которое больше данного в 1 000 раз, необходимо начальное число умножить на 1 000.
Краткое условие: Объясни, как можно сравнить два числа.
1) Из двух чисел меньше то, которое при счёте называют раньше, и больше то, которое называют позже.
2) Сравнивая числа поразрядно, начиная с высших разрядов, больше то число, в котором больше разрядов.
Если числа состоят из одинакового количества разрядов, то больше то число, у которого цифра высшего разряда больше.
Чтобы сравнить два числа, нужно сначала сравнить количество цифр в каждом числе. Больше то число, в котором больше цифр. Если количество цифр одинаково, необходимо сравнить каждую цифру слева направо поразрядно.
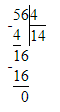
Страница 35. Что узнали. Чему научились. Номер: 12, 13, 14, 15, 16, 17, 1, 2, 3, 4, 5, 6, 7, задача на полях.



