ГДЗ 4 класс Математика Моро, Бантова, Бельтюкова

4класс

Страница 28, ГДЗ по математике за 4 класс к учебнику Моро часть 1

Выберите номер:

Задача на полях 129 130 131 132 133 134 135 136 137 Задача на полях Ребус

Номер задания: Задача на полях

Краткое условие: Сравни числа в каждом столбике. Что обозначает цифра 3 в записи чисел 3, 30, 300, 3 000? Во сколько раз 30 больше, чем 3? 300 больше, чем 3? 3 000 больше, чем 3? 300 больше, чем 30?

Решение:

1) Рассмотрим столбики чисел. Сравним числа в каждом столбике:

В каждом столбике каждое следующее число в 10 раз больше предыдущего.
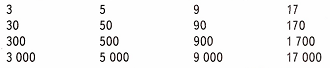
2) Подумаем, что обозначает цифра 3 в записи чисел:
1. 3 – цифра 3 обозначает количество единиц;
2. 30 – цифра 3 обозначает количество десятков;
3. 300 – цифра 3 обозначает количество сотен;
4. 3 000 – цифра 3 обозначает количество тысяч;
3) Подумаем, во сколько раз 30 больше, чем 3:
30 : 3 = 10;
Соответственно, 30 больше, чем 3 в 10 раз.
4) Подумаем, во сколько раз 300 больше, чем 3:
300 : 3 = 100;

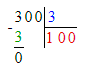
Соответственно, 300 больше, чем 3 в 100 раз.
5) Подумаем, во сколько раз 300 больше, чем 30:
300 : 30 = 10;

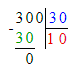
Соответственно, 300 больше, чем 30 в 10 раз.
6) Подумаем, во сколько раз 900 меньше, чем 9 000:
9 000 : 900 = 10;

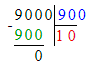
Соответственно, 900 меньше, чем 9 000 в 10 раз.
7) Подумаем, во сколько раз 90 меньше, чем 9 000:
9 000 : 90 = 100;

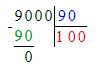
Соответственно, 90 меньше, чем 9 000 в 100 раз.
8) Подумаем, во сколько раз 9 меньше, чем 9 000:
9 000 : 9 = 1 000;

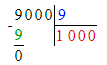
Соответственно, 9 меньше, чем 9 000 в 1 000 раз.
9) Закончим выводы:
1. Если в записи числа справа приписать 1 нуль, то получим число, которое больше данного в 10 раз.
2. Если в записи числа справа приписать 2 нуля, то получим число, которое больше данного в 100 раз.
3. Если в записи числа справа приписать 3 нуля, то получим число, которое больше данного в 1 000 раз.
4. Если в записи числа отбросить 1 нуль, то получим число, которое меньше данного в 10 раз.
5. Если в записи числа отбросить 2 нуля, то получим число, которое меньше данного в 100 раз.
6. Если в записи числа отбросить 3 нуля, то получим число, которое меньше данного в 1 000 раз.

Номер задания: 129

Краткое условие: 1) Числа 57, 90, 200 увеличь в 10 раз; в 100 раз.2) Числа 4 000, 60 000, 152 000 уменьши в 1 000 раз.

Решение:

1) 57∙10=570;
57∙100=5 700;
90∙10=900;
90∙100=9 000;
200∙10=2 000;
200∙100=20 000.
2) 4 000÷1 000=4;
60 000÷1 000=60;
152 000÷1 000=152.

Решение:

1)
1. Число 57 увеличим в 10 раз:
57 · 10 = 570;

2. Число 90 увеличим в 10 раз:
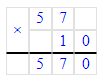
90 · 10 = 900;

3. Число 200 увеличим в 10 раз:
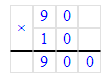
200 · 10 = 2 000;

4. Число 57 увеличим в 100 раз:
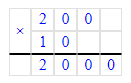
57 · 100 = 5 700;

5. Число 90 увеличим в 100 раз:
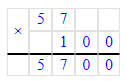
90 · 100 = 9 000;

6. Число 200 увеличим в 100 раз:
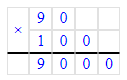
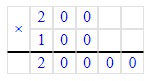
200 · 100 = 20 000;

2)
1. Число 4 000 уменьшим в 1 000 раз:
4 000 : 1 000 = 4;

2. Число 60 000 уменьшим в 1 000 раз:
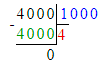
60 000 : 1 000 = 60;

3. Число 152 000 уменьшим в 1 000 раз:
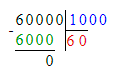
152 000 : 1 000 = 152;

Ответ:

1) 570; 900; 2 000; 5 700; 9 000; 20 000; 2) 4; 60; 152.

Номер задания: 130

Решение:

67 000÷1 000=67;
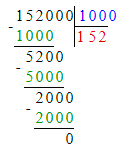
9 600÷100=96;
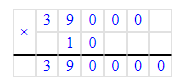
39 000∙10=390 000;
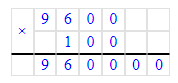
9 600∙100=960 000;
102 000÷100=1 020.

Решение:

1) 67 000 : 1 000 = 67;

2) 9 600 : 100 = 96;

3) 39 000 · 10 = 390 000;

4) 9 600 · 100 = 960 000;

5) 102 000 : 10 = 10 200;

6) 102 000 : 100 = 1 020;

Ответ:

1) 67; 2) 96; 3) 390 000; 4) 960 000; 5) 10 200; 6) 1 020.

Номер задания: 131

Решение:

99 999<100 000;
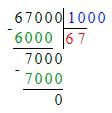
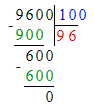
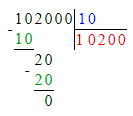
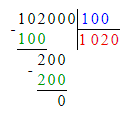
415 760>415 670.

Решение:

Сравним числа:
1) 99 999 и 100 000;
Данные числа необходимо сравнивать по старшему разряду.
Так как в числе 99 999 отсутствует разряд сотен тысяч, а в числе 100 000 данный разряд присутствует, то 99 999 < 100 000;
2) 415 760 и 415 670;
Данные числа необходимо сравнивать поразрядно.
Так как 7 > 6, то 415 760 > 415 670;

Номер задания: 132

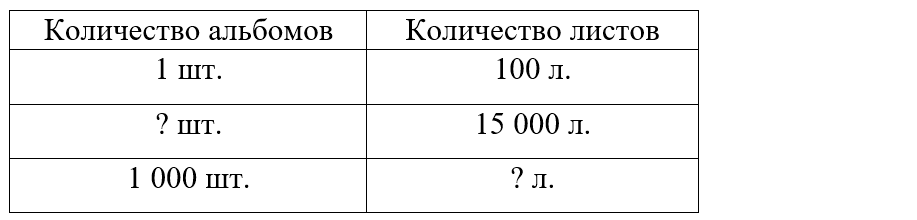
Краткое условие: Сколько альбомов по 100 листов получится из 15 000 листов? Сколько листов в 1 000 таких альбомов?

Дано:

В альбоме – 100 листов;
Из 15 000 листов -? альбомов;
? листов из 1000 альбомов.

Решение:

1) 15 000÷100=150(альбомов)- из 15 000 листов;
2) 1000∙100=100 000(листов) в 1000 альбомах.

Ответ:

150 альбомов; 100 000 листов.

Подсказка

Чтобы решить задачу, нужно:
ШАГ 1. Найти сколько получится альбомов из 15 000 листов.
ШАГ 2. Найти сколько листов в 1 000 альбомов.

Дано:

Решение:

Шаг 1. Найдём сколько получится альбомов из 15 000 листов:
1) 15 000 : 100 = 150 а. – столько альбомов получится из 15 000 листов

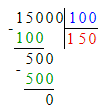
Шаг 2. Найдём сколько будет листов в 1 000 альбомов:
2) 100 · 1 000 = 100 000 л. – столько листов в 1 000 альбомов

Ответ:

из 15 000 листов получится 150 альбомов; в 1 000 альбомов 100 000 листов.

Под запись в тетрадь:

1) 15 000 : 100 = 150 (а.)
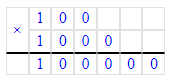
2) 100 · 1 000 = 100 000 (л.)
Ответ: из 15 000 листов получится 150 альбомов; в 1 000 альбомов 100 000 листов.

Номер задания: 133

Краткое условие: Чем похожи и различаются уравнения каждой пары и их решения?

Решение:

Уравнения первой пары похожи числами, но различаются действиями и ответами:
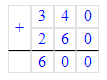
x-260=340;x=340+260;x=600.
x+260=340;x=340-260;x=80.
Уравнения второй пары похожи числами, но различаются действиями и ответами:
96÷x=4;x=96÷4;x=24.

96-x=4;x=96-4;x=92.
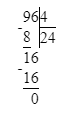
Уравнения третьей пары похожи числами, но различаются действиями и ответами:
16+x=80;x=80-16;x=64.
16∙x=80;x=80÷16;x=5.

Решение:

Сравним пары уравнений и сравним их решения:
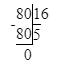
1)
1. х – 260 = 340;
х = 340 + 260;

х = 600;
2. х + 260 = 340;
х = 340 - 260;

х = 80;
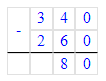
В первом уравнении необходимо найти уменьшаемое, а во втором уравнении – первое слагаемое. Первое уравнение решается с помощью сложения, а второе уравнение решается с помощью вычитания.
2)
1. 96 : х = 4;
х = 96 : 4;

х = 24;
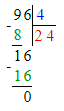
2. 96 - х = 4;
х = 96 - 4;

х = 92;
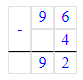
В первом уравнении необходимо найти делитель, а во втором уравнении – вычитаемое. Первое уравнение решается с помощью деления, а второе уравнение решается с помощью вычитания.
3)
1. 16 + х = 80;
х = 80 - 16;

х = 64;
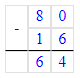
2. 16 · х = 80;
х = 80 : 16;

х = 5;
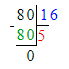
В первом уравнении необходимо найти второе слагаемое, а во втором уравнении – второй множитель. Первое уравнение решается с помощью вычитания, а второе уравнение решается с помощью деления.

Ответ:

1) 600; 80; 2) 24; 92; 3) 64; 5.

Номер задания: 134

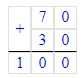
Краткое условие: Длина участка 70 м, ширина 30 м. Сколько шагов нужно сделать по периметру? (Два шага — 1 м.)

Дано:

Длина- 70 м;
Ширина – 30 м;
2 шага – 1м;
Р-?
Сколько шагов-?

Решение:

1) Р=(70+30)∙2=200 (м)-периметр;
2) 200∙2=400 (шагов)- надо сделать, чтобы пройти по периметру.

Ответ:

400 шагов.

Подсказка

Чтобы решить задачу, нужно:
ШАГ 1. Найти периметр участка.
ШАГ 2. Найти общее количество шагов.

Дано:

Решение:

Шаг 1. Найдём периметр участка:
1) Р = (70 + 30) · 2 = 100 · 2 = 200 м – периметр участка

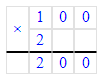
Шаг 2. Найдём общее количество шагов:
2) 200 · 2 = 400 ш. – всего шагов

Ответ:

чтобы пройти участок по периметру, необходимо сделать 400 шагов.

Под запись в тетрадь:

1) (70 + 30) · 2 = 200 (м)
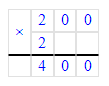
2) 200 · 2 = 400 (ш.)
Ответ: чтобы пройти участок по периметру, необходимо сделать 400 шагов.

Номер задания: 135

Краткое условие: Начерти: 1) отрезок AB, равный половине отрезка 1 дм; 2) отрезок CD, половина которого 2 см.

Дано:

Отрезок АВ равен половине отрезка в 1 дм.

Решение:

1 дм=10 см;
АВ=10÷2=5(см)

Дано:

Отрезок CD, длина половины которого равна 2 см.

Решение:

CD=2∙2=4(см)

Решение:

Начертим:
1) Отрезок АВ, длина которого равна половине длины отрезка в 1 дм:
1. 1 дм = 10 см;
2. Найдём длину отрезка АВ:
АВ = 10 см : 2 = 5 см;
3. Начертим отрезок АВ:

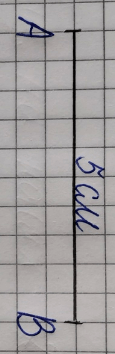
2) Отрезок CD, длина половины которого равна 2 см:
1. Найдём длину отрезка CD:
CD = 2 см · 2 = 4 см;
2. Начертим отрезок CD:

Номер задания: 136

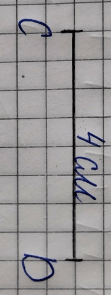
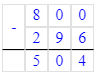
Краткое условие: Верны ли равенства? Проверь вычислениями.

Решение:

Проверим: 800-296=168∙3
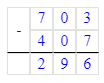
800-296=504;

168∙3=504.

Так как 504=504, то равенство верно.

Проверим: 888÷3=703-407
888÷3=296;

703-407=296.

Так как 296=296, то равенство верно.

Решение:

Проверим, верны ли равенства:
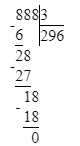
1) 800 – 296 = 168 · 3;
1. Сначала вычислим значение выражения слева:
800 – 296 = 504;

2. Далее вычислим значение выражения справа:
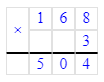
168 · 3 = 504;

3. Сравним полученные результаты:
Так как 504 = 504, то начальное неравенство верно.
2) 888 : 3 = 703 - 407;
1. Сначала вычислим значение выражения слева:
888 : 3 = 296;

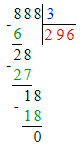
2. Далее вычислим значение выражения справа:
703 - 407 = 296;

3. Сравним полученные результаты:
Так как 296 = 296, то начальное неравенство верно.

Ответ:

1) верно; 2) верно.

Номер задания: 137

Краткое условие: Записали подряд все трёхзначные числа. Сколько всего цифр записано?

Решение:

От 100 до 999 всего 900 чисел (999-100+1=900).
В каждом числе по три цифры.
Таким образом, если записать все эти числа подряд, то получится 900∙3=2700 (цифр)- в этом ряду.

Ответ:

2 700 цифр.

Решение:

Подумаем, сколько всего цифр записано в ряду при условии, что записали подряд все трехзначные числа:
Наименьшее трёхзначное число – 100, а наименьшее четырёхзначное число – 1 000. Найдём количество всех трёхзначных чисел:
1 000 – 100 = 900;

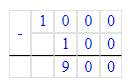
Следовательно, всего 900 трехзначных чисел. В каждом трехзначном числе 3 цифры. Найдем, сколько всего цифр во всех трехзначных числах:
900 · 3 = 2 700

Соответственно, во всех трехзначных числах 2 700 цифр.

Ответ:

2 700 цифр.

Номер задания: Задача на полях

Решение:

1) 34 800 : 10 = 3 480;

2) 4 900 : 100 = 49;

3) 540 · 10 = 5 400;

Ответ:

1) 3 480; 2) 49; 3) 5 400.

Номер задания: Ребус

Решение:

1) Рассмотрим ребус:

2) Разгадаем ребус:
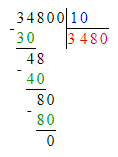
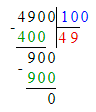
1. Так как при делении одинаковых чисел получается такое же число, то за квадратом скрывается число 1.
Следовательно, 1 : 1 = 1.
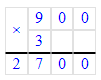
2. Если неизвестное число умножить на 1 и в результате получится 7, то треугольник равен:
х · 1 = 7;
х = 7 : 1;
х = 7;
За треугольником скрывается число 7.
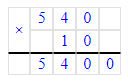
3. Найдем значение последнего выражения, разделив значение треугольника на значение квадрата:
7 : 1 = 7;

Ответ:

квадрат = 1; треугольник = 7; 7 : 1 = 7.

Страница 27 Страница 29