Страница 26, ГДЗ по математике за 4 класс к учебнику Моро часть 1
Страница 26
Краткое условие: Замени числа суммой разрядных слагаемых.
205 000=200 000+5 000;
205 040=200 000+5000+40;
1 648=1 000+600+40+8;
640 008=600 000+40 000+8;
164 800=100 000+600 000+4 000+800.
1) 205 = 200 + 5;
2) 205 000 = 200 000 + 5 000;
3) 205 040 = 200 000 + 5 000 + 40;
4) 1 648 = 1 000 + 600 + 40 + 8;
5) 640 008 = 600 000 + 40 000 + 8;
6) 164 800 = 100 000 + 60 000 + 4 000 + 800;
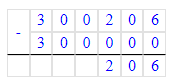
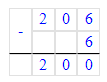
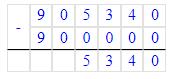
300 206-300 000-6=200.
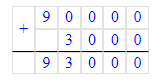
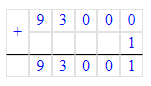
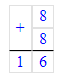
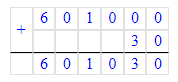
1) 90 000 + 3 000 + 1 = 93 000 + 1 = 93 001;
Краткое условие: Сколько цифр потребуется для записи шестизначного числа? пятизначного?
Для записи числа, высший разряд которого десятки тысяч потребуется 5 цифр.
Если высшим разрядом числа являются сотни тысяч, то для записи числа потребуется 6 цифр.
2) Подумаем, сколько цифр потребуется для записи числа, высший разряд которого – десятки тысяч:
Если высшим разрядом числа являются десятки тысяч, то для записи числа потребуется 5 цифр.
Краткое условие: Вставь числа, пропущенные при счёте.
9 997, 9 998, 9 999, 10 000, 10 001, 10 002.
Краткое условие: Выпиши равные отрезки, найди периметр и площадь прямоугольника ABCD.
BC=AD=3 см;
P-?
S-?
2) S=5∙3=15 (см2)
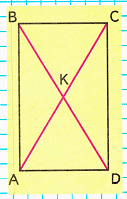
1. ВС = АD;
2. АВ = СD;
3. АК = КС = ВК = КD;
3) Найдем периметр прямоугольника АВСD:
1. ВС = АD = 3 см;
2. АВ = СD = 5 см;
3. РАВСD = АВ + ВС + СD + АD = 5 + 3 + 5 + 3 = 8 + 8 = 16 см;
SАВСD = АВ · ВС = 5 · 3 = 15 см2;
Краткое условие: Составь и реши задачу.
ШАГ 1. Найти количество дней, за которые было израсходовано 80 кг муки.
За 1 день в пекарне расходуется 10 кг муки. За время работы пекарни было израсходовано 80 кг муки. Сколько дней работала пекарня?
2) Решим задачу:

1) 80 : 10 = 8 дн. – дни, за которые израсходовали 80 кг муки
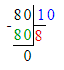
Ответ: 80 кг муки израсходовали за 8 дней.
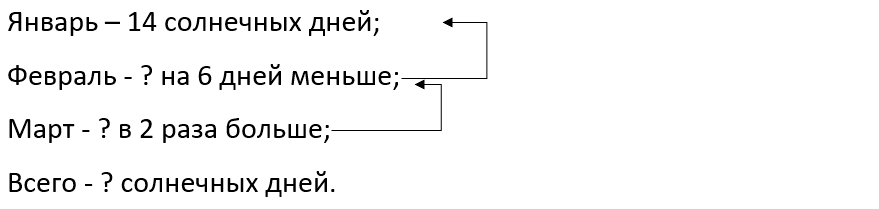
Краткое условие: В январе было 14 солнечных дней, в феврале на 6 меньше, а в марте в 2 раза больше, чем в феврале. Задай вопрос и реши задачу.
2) 8∙2=16 (дней)- солнечных было в марте;
3) 14+16+8=38 (дней)- солнечных было за 3 месяца.
ШАГ 1. Найти количество солнечных дней в феврале.
ШАГ 2. Найти количество солнечных дней в марте.
В январе было 14 солнечных дней, в феврале – на 6 дней меньше, чем в январе, а в марте – в 2 раза больше, чем в феврале. Сколько солнечных дней было в марте?
2) Решим задачу:

1) 14 - 6 = 8 дн. – в феврале
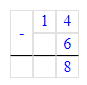
2) 8 · 2 = 16 дн. – в марте
2) 8 · 2 = 16 (дн.)
Ответ: в марте было 16 солнечных дней.
Краткое условие: Построй диаграмму солнечных дней по месяцам (2 дня — 1 клетка).
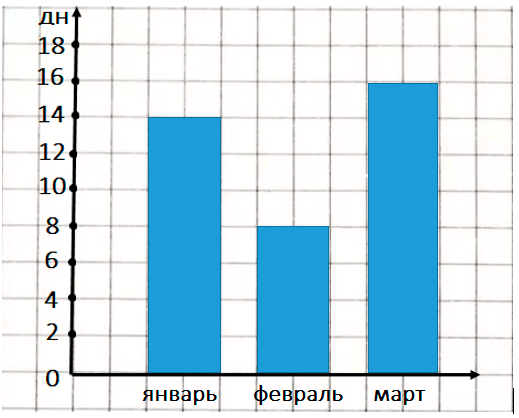
14÷2=7 (клеток)- январь;
8÷2=4 (клетки)- февраль;
16÷2=8 (клеток) - март.

Краткое условие: Проверь, верны ли неравенства. Исправь ошибки.
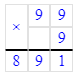 891>691.
891>691.
Проверим: 207∙4>820- верно.
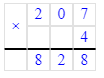 828>820.
828>820.
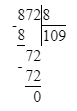 209>109.
209>109.
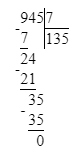 125<135.
125<135.
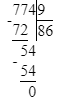 68<86.
68<86.
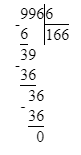 160<166.
160<166.
1) 99 · 9 < 691;
1. Сначала вычислим значение выражения слева:
99 · 9 = 891;

Так как 891 > 691, то 99 · 9 > 691 и начальное неравенство неверно.
2) 207 · 4 > 820;
1. Сначала вычислим значение выражения слева:
207 · 4 = 828;

Так как 828 > 820, то 207 · 4 > 820 и начальное неравенство верно.
3) 209 > 872 : 8;
1. Сначала вычислим значение выражения справа:
872 : 8 = 109;
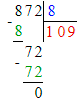
Так как 209 > 109, то 209 > 872 : 8 и начальное неравенство верно.
4) 125 < 945 : 7;
1. Сначала вычислим значение выражения справа:
945 : 7 = 135;
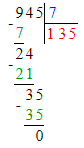
Так как 125 < 135, то 125 < 945 : 7 и начальное неравенство верно.
5) 68 < 774 : 9;
1. Сначала вычислим значение выражения справа:
774 : 9 = 86;
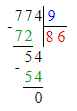
Так как 68 < 86, то 68 < 774 : 9 и начальное неравенство верно.
6) 160 > 996 : 6;
1. Сначала вычислим значение выражения справа:
996 : 6 = 166;
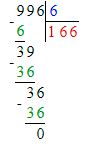
Так как 160 < 166, то 160 < 996 : 6 и начальное неравенство неверно.
Краткое условие: Узнай числа под фигурами, помня, что одинаковые фигуры — одинаковые числа.
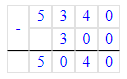
Так как треугольник (70) плюс квадрат равно 120, то квадрат равен 120-70=50.
Так как квадрат (50) плюс круг равно 230, то круг равен 230-50=180.

1. Найдём, какое число прячется за треугольником, решив третье выражение:
х + 230 = 300;
х = 300 – 230;
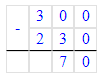
2. Найдём, какое число прячется за квадратом, решив первое выражение и подставив найденное значение:
70 + х = 120;
х = 120 – 70;
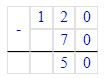
3. Найдём, какое число прячется за кругом, решив второе выражение и подставив найденное значение:
50 + х = 230;
х = 230 – 50;
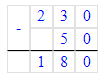
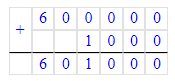
Страница 26. Номер: 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, задача на полях.



