Страница 14, ГДЗ по математике за 4 класс к учебнику Моро часть 1
Страница 14
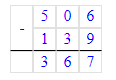
Краткое условие: Продолжи объяснение.
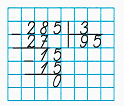
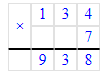
1. Делю сотни. 2 сотни нельзя разделить на 3 так, чтобы в частном получились сотни.
2. Делю десятки. 2 сотни и 8 десятков – это 28 десятков. Неполное частное чисел 28 и 3 равняется 9. Умножаем 9 на 3, получаем 27. Разделили 27 десятков. Осталось разделить 1 десяток. Сравниваем остаток с делителем: число оставшихся десятков меньше, чем 3, значит, можно продолжать деление.
3. Делю единицы. 1 десяток и 5 единиц – это 15 единиц. Частное чисел 15 и 3 равняется 5. Умножаем 5 на 3, получаем 15. Разделили 15 единиц. Единицы разделили все.
4. Читаю ответ: 95.
Краткое условие: Объясни, как разделили 128 на 4.
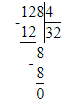
Делю десятки. 1 сотня и 2 десятка-это 12 десятков. Разделю 12 на 4. В частном будет 3 десятка.
Умножаю 3∙4=12. Вычитаю 12-12=0. Осталось разделить 8 единиц на 4, будет 2 единицы. Умножаю 2∙4=8 Вычитаю 8-8=0.
Деление закончилось.
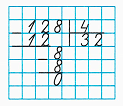
2. Делю десятки. 1 сотня и 2 десятка – это 12 десятков. Частное чисел 12 и 4 равняется 3. Умножаем 3 на 4, получаем 12. Разделили 12 десятков. Десятки разделили все, можно продолжать деление.
3. Делю единицы. Частное чисел 8 и 4 равняется 2. Умножаем 2 на 4, получаем 8. Разделили 8 единиц. Единицы разделили все.
4. Читаю ответ: 32.
Краткое условие: Выполни деление и проверь умножением.
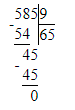
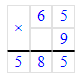
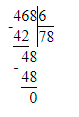
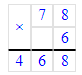
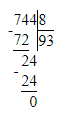
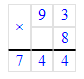
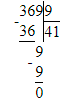
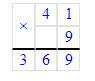
1) 585 : 9 = 65;
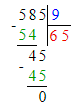

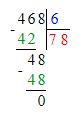

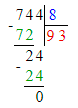

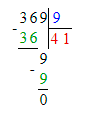

Краткое условие: В 4 канистры помещается 80 л бензина. Сколько литров поместится в 3 канистры? Сколько таких канистр нужно для 100 л?
В 3канистры -? л бензина;
? канистр для 100 л бензина.
2) 20∙3=60 (л)- бензина входит в 3 канистры;
3) 100÷20=5 (канистр)- потребуется для 100 л бензина.
ШАГ 1. Найти вместимость 1 канистры.
ШАГ 2. Найти вместимость 3 канистр.
ШАГ 3. Найти количество канистр для 100 л бензина.

1) 80 : 4 = 20 л – вместимость 1 канистры
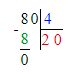
2) 20 · 3 = 60 л – вместимость 3 канистр
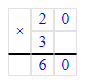
3) 100 : 20 = 5 к. – столько канистр необходимо для 100 л бензина
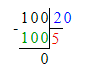
2) 20 · 3 = 60 (л)
3) 100 : 20 = 5 (к.)
Ответ: в 3 канистры поместится 60 л бензина; для 100 л бензина необходимо 5 канистр.
Краткое условие: Хватит ли 100 л бензина для поездки туда и обратно, если в одну сторону требуется 48 л? А 90 л?
Хватит ли для поездки туда и обратно 100 л бензина?
Хватит ли для поездки туда и обратно 90 л бензина?
2) 100л>98 л, значит для поездки от посёлка до города и обратно хватит 100 л бензина;
3) 90л<98 л, значит для поездки от посёлка до города и обратно не хватит 90 л бензина;
ШАГ 1. Найти количество бензина, необходимого для поездки в обе стороны.
ШАГ 2. Сравнить данное количество со 100 л бензина.
ШАГ 3. Сравнить данное количество с 90 л бензина.

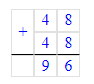
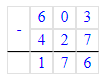
1) 48 + 48 = 96 л – необходимо на дорогу в обе стороны
2) 96 л < 100 л – следовательно, 100 л хватит Шаг 3. Подумаем, хватит ли 90 л бензина на эту дорогу:
3) 96 л > 90 л – следовательно, 90 л не хватит
2) 96 л < 100 л – хватит
3) 96 л > 90 л – не хватит
Ответ: 100 л бензина хватит; 90 л бензина не хватит.
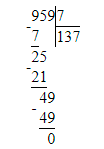
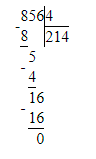
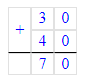
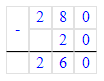
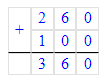
280-40÷2+100=280-20+100=260+100=360.


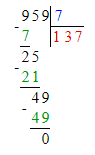
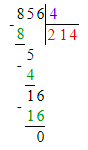


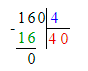
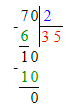
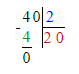
Краткое условие: 1) Поставь скобки так, чтобы выражение 53-3-9+4-6 стало равно: 2; 50; 180; 474.
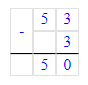
53-(3∙9+4∙6)=53-(27+24)=53-51=2;
(53-3∙9)+4∙6=(53-27)+4∙6=26+24=50;
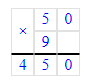
(53-3∙9+4)∙6=(53-27+4)∙6=30∙6=180;
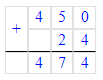
(53-3)∙9+4∙6=50∙9+24=450+24=474.
2)
В группе букв можно провести ось симметрии:

53 – 3 · 9 + 4 · 6 стало равно:
1. 2;
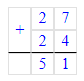
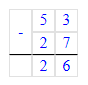
Чтобы значение выражения стало равным 2, необходимо скобки расставить следующим образом:


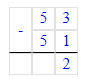
Чтобы значение выражения стало равным 50, необходимо скобки расставить следующим образом:


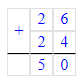
Чтобы значение выражения стало равным 180, необходимо скобки расставить следующим образом:

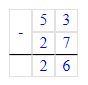
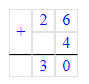
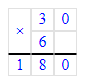
Чтобы значение выражения стало равным 474, необходимо скобки расставить следующим образом:


Краткое условие: Вычисли.
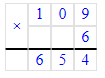
1) 672 : 7 = 96;
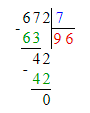
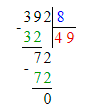
Страница 14. Номер: 69, 70, 71, 72, 73, 74, задача на полях.



