Страница 99, ГДЗ по математике за 3 класс к учебнику Моро часть 1
Страница 99
Краткое условие: 1) В году три осенних месяца: сентябрь, октябрь и ноябрь. Узнай по календарю, сколько дней длится осень; сколько недель она длится. 2) Используя календарь, составь и реши похожие задачи про зиму, весну и лето.
30 + 31 + 30 = 91 (день) - длится осень.
Осень длится 13 недель.
2)
Задача 1: Узнай по календарю, сколько дней длится зима; сколько недель она длится.
31 + 31 + 28 = 90 (дней) - длится зима.
Зима длится 13 недель.
Задача 2: Узнай по календарю, сколько дней длится весна; сколько недель она длится.
31 + 30 + 31 = 92 (дня) - длится весна.
Весна длится 13 недель и 1 день.
Задача 3: Узнай по календарю, сколько дней длится лето; сколько недель она длится.
30 + 31 + 31 = 92 (дня) - длится лето.
Лето длится 13 недель и 1 день.
Осень длится 92 дня, что составляет 13 недель.
2) Используя календарь, составим и решим похожие задачи про зиму, весну и лето:
1. В году три зимних месяца: декабрь, январь, февраль. Узнай по календарю, сколько дней длится зима; сколько недель она длится.
Краткое условие: Назови время, которое показывают часы, используя слова «четверть» и «половина».
2 часы показывают без четверти час.
3 часы показывают половина первого.
1) Рассмотрим первые часы:
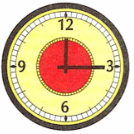
Часы показывают четверть первого.
2) Рассмотрим вторые часы:
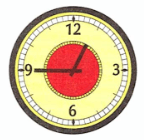
Часы показывают без четверти час.
3) Рассмотрим третьи часы:
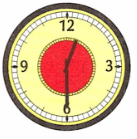
Часы показывают половину первого.
Краткое условие: Таня отрезала от ленты её пятую часть — 8 дм. Найди длину всей ленты в дециметрах и вырази её в метрах.
Длина ленты - ? дм = ? м.
ШАГ 1. Найти длину всей ленты.

1) 8 ∙ 5 = 40 дм = 4 м – длина всей ленты
Ответ: длина всей ленты равна 4 м.
Краткое условие: Петя купил упаковку корма для попугая. В упаковке 27 пакетиков. На сколько недель хватит попугаю этого корма, если каждую неделю он съедает по 3 пакетика корма?
3 пакетика – 1 неделя.
ШАГ 1. Найти на сколько недель хватит попугаю этого корма.

1) 27 : 3 = 9 н. – на столько недель хватит корма
Ответ: на 9 недель хватит попугаю корма.
Краткое условие: Проверь, правильно ли решены уравнения.
y = 7
Проверка:
7 ∙ 6 = 42
42 = 42
x = 49
Проверка:
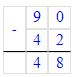
56 ÷ 49 ≠ 7
x = 56
Проверка:
56 ÷ 9 ≠ 6
1) у ∙ 6 = 42;
у = 42 : 6;
у = 7;
7 = 7;
Значит, уравнение решено правильно.
2) 56 : х = 7;
х = 56 : 7;
х = 8;
8 ≠ 49;
Значит, уравнение решено неправильно.
3) х : 9 = 6;
х = 6 • 9;
х = 54;
54 ≠ 56;
Значит, уравнение решено неправильно.
6 ∙ 4 ÷ 3 = 24 ÷ 3 = 8;
9 ∙ 4 ÷ 6 = 36 ÷ 6 = 6;
14 ÷ 2 ∙ 7 = 7 ∙ 7 = 49;
27 ÷ 3 ∙ 9 = 9 ∙ 9 = 81;
32 ÷ 4 ∙ 8 = 8 ∙ 8 = 64;
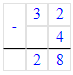
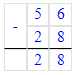
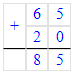
56 - (32 - 4) = 56 - 28 = 28;
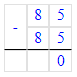
85 - (65 + 20) = 85 - 85 = 0;
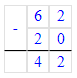
90 - (62 - 20) = 90 - 42 = 48;
0 ÷ 9 = 0;
0 ÷ 24 = 0;
0 ∙ 33 = 0.
ШАГ 1. Выполняем действия в скобках.
ШАГ 2. Выполняем умножение и деление по порядку.
ШАГ 3. Выполняем сложение и вычитание по порядку.
11) 0 : 24 = 0;
12) 0 ∙ 33 = 0;
Краткое условие: 1) Из чисел б, 2, 15 и 5 составь две суммы так, чтобы значение одной суммы было в 3 раза меньше значения другой. 2) Из тех же чисел составь две разности так, чтобы значение одной разности было в 3 раза больше значения другой.
15 + 6 = 21 и 2 + 5 = 7
21 ÷ 7 = в 3 (раза) - 7 меньше 21.
Значит сумма чисел 2 и 5 в 3 раза меньше суммы 15 и 6.
2)
15 - 6 = 9 и 5 - 2 = 3
9 ÷ 3 = в 3 (раза) - 9 больше 3.
Значит разность чисел 15 и 6 в 3 раза больше разности 5 и 2.
1. 15 + 6 = 21;
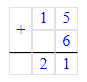
2. 6 + 2 = 8;
Так как 27 : 7 = 3, значит, две суммы составили верно.
2) Из тех же чисел составим две разности так, чтобы значение одной разности было в 3 раза больше значения другой:
1. 15 – 6 = 9;
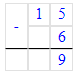
2. 5 – 2 = 3;
Так как 9 : 3 = 3, значит, две разности составили верно.
Краткое условие: Какую часть года составляют 3 месяца?
1 год = 12 месяцев;
12 : 3 = 4;
Значит, 3 месяца составляют одну четвёртую часть года.
2) Наберем множителями число 24:
1. 6 • 4 = 24;
2. 24 • 1 = 24;
3. 8 • 3 = 24;



