3класс
Страница 85, ГДЗ по математике за 3 класс к учебнику Моро часть 1
Выберите номер:
Номер задания: 7
Краткое условие: Реши уравнения.
Решение:
75 + x = 90
x = 90 - 75
x = 15
75 + 15 = 90
90 = 90
x = 90 - 75
x = 15
75 + 15 = 90
90 = 90
Ответ:
x = 15
80 - k = 42
k = 80 - 42
k = 38
80 - 38 = 42
42 = 42
k = 80 - 42
k = 38
80 - 38 = 42
42 = 42
Ответ:
k = 38
6 ∙ n = 54
n = 54 ÷ 6
n = 9
6 ∙ 9 = 54
54 = 54
n = 54 ÷ 6
n = 9
6 ∙ 9 = 54
54 = 54
Ответ:
n = 9
Решение:
Решим уравнения:
1) 75 + х = 90;
х = 90 – 75;
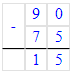
х = 15;
2) 80 – k = 42;
k = 80 – 42;
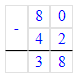
k = 38;
3) 6 ∙ n = 54;
n = 54 : 6;
n = 9;
1) 75 + х = 90;
х = 90 – 75;
х = 15;
2) 80 – k = 42;
k = 80 – 42;
k = 38;
3) 6 ∙ n = 54;
n = 54 : 6;
n = 9;
Ответ:
1) 15; 2) 38; 3) 9.
Номер задания: 8
Краткое условие: 1) Найди площадь прямоугольника ВСКЕ и площадь прямоугольника AEKD. 2) Найди площадь прямоугольника ABCD. Сколькими способами это можно сделать?
Решение:
1) Прямоугольник BCKE:
2 ∙ 2 = 4 (см²) - площадь.
Прямоугольник AEKD:
2 ∙ 3 = 6 (см²) - площадь.
2) Прямоугольник ABCD:
1 способ: измеряем длины BC и CD и находим площадь:
2 ∙ 5 = 10 (см²) - площадь.
2 способ: сложить площадь прямоугольников BCKE и AEKD:
4 + 6 = 10 (см²) - площадь.
2 ∙ 2 = 4 (см²) - площадь.
Прямоугольник AEKD:
2 ∙ 3 = 6 (см²) - площадь.
2) Прямоугольник ABCD:
1 способ: измеряем длины BC и CD и находим площадь:
2 ∙ 5 = 10 (см²) - площадь.
2 способ: сложить площадь прямоугольников BCKE и AEKD:
4 + 6 = 10 (см²) - площадь.
Ответ:
10 см² площадь ABCD.
Решение:
1) Рассмотрим чертёж:
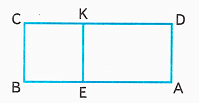
2) Найдём площадь прямоугольника ВСКЕ:
1. ВС = СК = КЕ = ВЕ = 2 см;
2. S = 2 • 2 = 4 (см²);
3) Найдём площадь прямоугольника АЕКD:
1. ЕК = 2 см;
2. АЕ = 3 см;
3. S = 2 • 3 = 6 (см²);
4) Найдём площадь прямоугольника АВСD:
S = 4 + 6 = 10 (см²);
5) Подумаем, сколькими способами это можно посчитать:
Вычислить площадь прямоугольника можно двумя способами:
1 способ
Найти сумму площадей двух прямоугольников: ВСКЕ и КЕDА.
2 способ
Вычислить площадь прямоугольника по формуле: умножить длину на ширину.
2) Найдём площадь прямоугольника ВСКЕ:
1. ВС = СК = КЕ = ВЕ = 2 см;
2. S = 2 • 2 = 4 (см²);
3) Найдём площадь прямоугольника АЕКD:
1. ЕК = 2 см;
2. АЕ = 3 см;
3. S = 2 • 3 = 6 (см²);
4) Найдём площадь прямоугольника АВСD:
S = 4 + 6 = 10 (см²);
5) Подумаем, сколькими способами это можно посчитать:
Вычислить площадь прямоугольника можно двумя способами:
1 способ
Найти сумму площадей двух прямоугольников: ВСКЕ и КЕDА.
2 способ
Вычислить площадь прямоугольника по формуле: умножить длину на ширину.
Ответ:
площадь прямоугольника ВСКЕ равна 4 см²; площадь прямоугольника АЕКD равна 6 см²; площадь прямоугольника АВСD равна 10 см².
Номер задания: 9
Краткое условие: 1) Сделай такой же чертёж в тетради и подумай, как можно узнать площадь каждой из фигур с общей стороной ОК (рис. 1); с общей стороной NP. 2) Узнай, площадь какой фигуры меньше: прямоугольника ВСКЕ или треугольника OKD — и на сколько квадратных сантиметров.
Решение:
1)
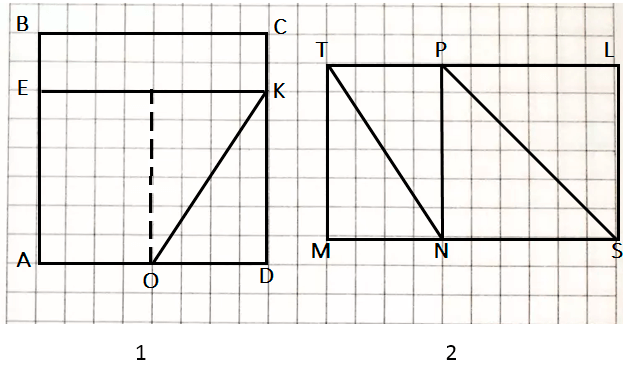
Находим площади через прямоугольник AEKD:
3 ∙ 4 = 12 (см²) - площадь.
Затем, делим площадь пополам (пунктир в точке О):
12 ÷ 2 = 6 (см²)
Теперь находим площадь треугольника OKD. Это прямоугольный треугольник, значит, делим пополам и получим площадь треугольника:
6 ÷ 2 = 3 (см²) - площадь OKD.
6 + 3 = 9 (см²) - площадь OKEA.
3 ∙ 3 = 9 (см²) - площадь NPLS.
2 ∙ 3 ÷ 2 = 3 (см²) - площадь NTP.
2)
1 ∙ 4 = 4 (см²) - площадь BCKE.
6 ÷ 2 = 3 (см²) - площадь OKD.
4 см² < 3 см² на 1 см².
Находим площади через прямоугольник AEKD:
3 ∙ 4 = 12 (см²) - площадь.
Затем, делим площадь пополам (пунктир в точке О):
12 ÷ 2 = 6 (см²)
Теперь находим площадь треугольника OKD. Это прямоугольный треугольник, значит, делим пополам и получим площадь треугольника:
6 ÷ 2 = 3 (см²) - площадь OKD.
6 + 3 = 9 (см²) - площадь OKEA.
3 ∙ 3 = 9 (см²) - площадь NPLS.
2 ∙ 3 ÷ 2 = 3 (см²) - площадь NTP.
2)
1 ∙ 4 = 4 (см²) - площадь BCKE.
6 ÷ 2 = 3 (см²) - площадь OKD.
4 см² < 3 см² на 1 см².
Ответ:
площадь прямоугольника на 1 см² больше площади треугольника.
Решение:
1) Рассмотрим чертеж:
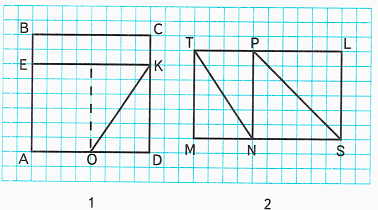
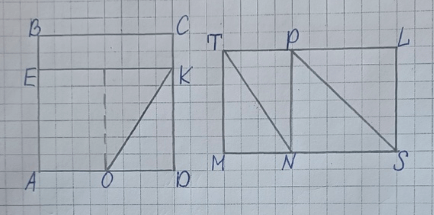
2) Сделаем такой же чертёж в тетради:
3) Подумаем, как можно узнать площадь каждой из фигур с общей стороной ОК:
1. Чтобы найти площадь треугольника ОКD, нужно сначала найти площадь прямоугольника, где сторона ОК является диагональю прямоугольника (для этого нужно перемножить длины сторон КD и ОD), а после полученный результат разделить на два.
2. Чтобы найти площадь четырёхугольника ЕКОА, нужно к площади прямоугольника, где сторона ОК является диагональю прямоугольника, прибавить площадь треугольника ОКD.
4) Подумаем, как можно узнать площадь каждой из фигур с общей стороной NP:
1. Чтобы найти площадь треугольника NPS, нужно сначала найти площадь квадрата NPLS (для этого нужно перемножить длины сторон NP и NS), а после полученный результат разделить на два.
2. Чтобы найти площадь треугольника NPТ, нужно сначала найти площадь прямоугольника NPТМ (для этого нужно перемножить длины сторон NP и РТ), а после полученный результат разделить на два.
5) Подумаем, площадь какой фигуры меньше: прямоугольника ВСКЕ или треугольника ОКD, и на сколько квадратных сантиметров:
1. Вычислим площадь прямоугольника ВСКЕ:
ВС = 4 см;
ВЕ = 1 см;
S = 4 • 1 = 4 (см²);
2. Вычислим площадь треугольника ОКD:
КD = 3 см;
ОD = 2 см;
S1 = 3 • 2 = 6 (см²);
SОКD = 6 : 2 = 3 (см²);
3. 4 – 3 = 1 (см²);
Следовательно, площадь треугольника ОКD меньше площади прямоугольника ВСКЕ на 1 см².
2) Сделаем такой же чертёж в тетради:
3) Подумаем, как можно узнать площадь каждой из фигур с общей стороной ОК:
1. Чтобы найти площадь треугольника ОКD, нужно сначала найти площадь прямоугольника, где сторона ОК является диагональю прямоугольника (для этого нужно перемножить длины сторон КD и ОD), а после полученный результат разделить на два.
2. Чтобы найти площадь четырёхугольника ЕКОА, нужно к площади прямоугольника, где сторона ОК является диагональю прямоугольника, прибавить площадь треугольника ОКD.
4) Подумаем, как можно узнать площадь каждой из фигур с общей стороной NP:
1. Чтобы найти площадь треугольника NPS, нужно сначала найти площадь квадрата NPLS (для этого нужно перемножить длины сторон NP и NS), а после полученный результат разделить на два.
2. Чтобы найти площадь треугольника NPТ, нужно сначала найти площадь прямоугольника NPТМ (для этого нужно перемножить длины сторон NP и РТ), а после полученный результат разделить на два.
5) Подумаем, площадь какой фигуры меньше: прямоугольника ВСКЕ или треугольника ОКD, и на сколько квадратных сантиметров:
1. Вычислим площадь прямоугольника ВСКЕ:
ВС = 4 см;
ВЕ = 1 см;
S = 4 • 1 = 4 (см²);
2. Вычислим площадь треугольника ОКD:
КD = 3 см;
ОD = 2 см;
S1 = 3 • 2 = 6 (см²);
SОКD = 6 : 2 = 3 (см²);
3. 4 – 3 = 1 (см²);
Следовательно, площадь треугольника ОКD меньше площади прямоугольника ВСКЕ на 1 см².
Ответ:
на 1 см² меньше.
Номер задания: Задача на полях
Краткое условие: На сколько 9 меньше, чем 72? Во сколько раз 6 меньше, чем 54?
Решение:
1) Подумаем, на сколько 9 меньше, чем 72:
72 – 9 = 63;
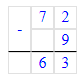
Следовательно, 9 на 63 меньше, чем 72.
2) Подумаем, во сколько раз 6 меньше, чем 54:
54 : 6 = 9;
Следовательно, 6 в 9 раз меньше, чем 54.
72 – 9 = 63;
Следовательно, 9 на 63 меньше, чем 72.
2) Подумаем, во сколько раз 6 меньше, чем 54:
54 : 6 = 9;
Следовательно, 6 в 9 раз меньше, чем 54.
Ответ:
1) на 63 меньше; 2) в 9 раз меньше.
Номер задания: Цепочка
Решение:
1) Рассмотрим цепочку:
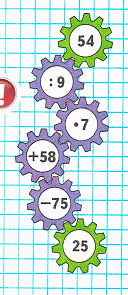
2) Заполним цепочку вычислений:
1. 54 : 9 = 6;
2. 6 • 7 = 42;
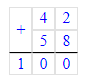
3. 42 + 58 = 100;
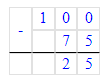
4. 100 – 75 = 25;
2) Заполним цепочку вычислений:
1. 54 : 9 = 6;
2. 6 • 7 = 42;
3. 42 + 58 = 100;
4. 100 – 75 = 25;
Ответ:
25.
Смотрите ещё задания из учебника:
Страница 79
Страница 80
Страница 81
Страница 82
Страница 83
Страница 87
Страница 88
Страница 89
Страница 90
Страница 92
... смотреть все номера
