Страница 67, ГДЗ по математике за 3 класс к учебнику Моро часть 1
75 + 81 ÷ 9 = 75 + 9 = 84;
38 - 64 ÷ 8 = 38 - 8 = 30;
30 - 12 ÷ 3 + 3 = 30 - 4 + 3 = 26 + 3 = 29;
30 - 12 ÷ (3 + 3) = 30 - 12 ÷ 6 = 30 - 2 = 28;
(30 - 12) ÷ 3 + 3 = 18 ÷ 3 + 3 = 6 + 3 = 9;
8 ∙ (13 - 7) = 8 ∙ 6 = 48;
9 ∙ (14 - 6) = 9 ∙ 8 = 72;
7 ∙ (12 - 3) = 7 ∙ 9 = 63.
ШАГ 1. Выполняем действия в скобках.
ШАГ 2. Выполняем умножение и деление по порядку.
ШАГ 3. Выполняем сложение и вычитание по порядку.
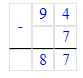
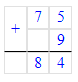
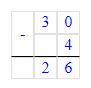
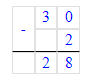
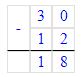
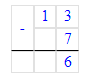
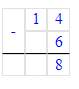
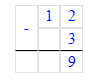
Краткое условие: 1) Маме 32 года, а сыну 8 лет. мама старше сына? 2) Во сколько раз мама была 5 лет назад?
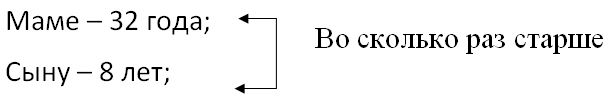
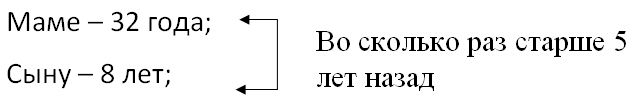
2) 8 - 5 = 3 (года) - сыну 5 лет назад;
3) 27 ÷ 3 = в 9 (раз) - мать старше сына 5 лет назад.
ШАГ 1. Найти во сколько раз мама старше сына.

1) 32 : 8 = 4 р. – во столько раз мама старше
Ответ: 1) мама старше сына в 4 раза; 2) 5 лет назад мама так же была старше сына в 4 раза.
Краткое условие: По таблице на обороте обложки учебника: 1) найди произведение: 6 * 7, 4 * 8, 9 * 3, 4 * 9; 2) проверь, что 7 * 8 = 8 * 7, 3 * 6 = 6 * 3; 3) найди частное: 54 : 9, 32 : 4, 42 : 6, 35 : 5; 4) назови числа от 6 до 60, которые делятся на 6; 5) назови числа от 4 до 40, которые делятся на 4.
2) 7 ∙ 8 = 8 ∙ 7; 56 = 56 - верно;
3 ∙ 6 = 6 ∙ 3; 18 = 18 - верно.
3) 54 ÷ 9 = 6; 32 ÷ 4 = 8; 42 ÷ 6 = 7; 35 ÷ 5 = 7.
4) Делятся на 6: 6, 12, 18, 24, 30, 36, 42, 54, 60.
5) Делятся на 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40.
1. 6 • 7 = 42;
2. 4 • 8 = 32;
3. 9 • 3 = 27;
4. 4 • 9 = 36;
2) Проверим:
1. 7 • 8 = 8 • 7;
Так как 7 • 8 = 56, а 8 • 7 = 56, то 56 = 56. Значит, равенство верно.
2. 3 • 6 = 6 • 3;
Так как 3 • 6 = 18, а 6 • 3 = 18, то 18 = 18. Значит, равенство верно.
3) Найдем частное:
1. 54 : 9 = 6;
2. 32 : 4 = 8;
3. 42 : 6 = 7;
4. 35 : 5 = 7;
4) Назовем числа от 6 до 60, которые делятся на 6:
6; 12; 18; 24; 30; 36; 42; 48; 54; 60;
5) Назовем числа от 4 до 40, которые делятся на 4:
4; 8; 12; 16; 20; 24; 28; 32; 36; 40;
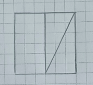
Краткое условие: 1) Начерти на листе клетчатой бумаги такой квадрат, вырежи его и разрежь по показанным на чертеже линиям. 2) Запиши номера фигур, которые ты сможешь выложить, используя полученные части квадрата. 3) Чему равна площадь каждой из этих фигур? 4) Верно ли, что все фигуры 1—5 будут сим-метричными?
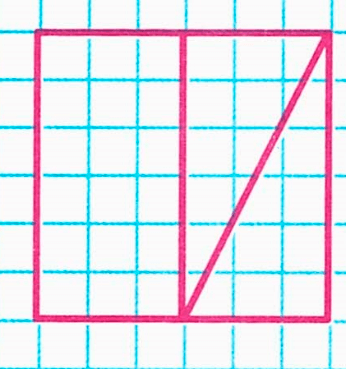
2) Используя части квадрата, можно выложить фигуры 1,3,5.
3) Площадь каждой фигуры будет одинаковой, потому что они составлены из частей одной фигуры, т.е. 3 ∙ 3 = 9 см².
4) Фигуры 1-5 будут симметричными.
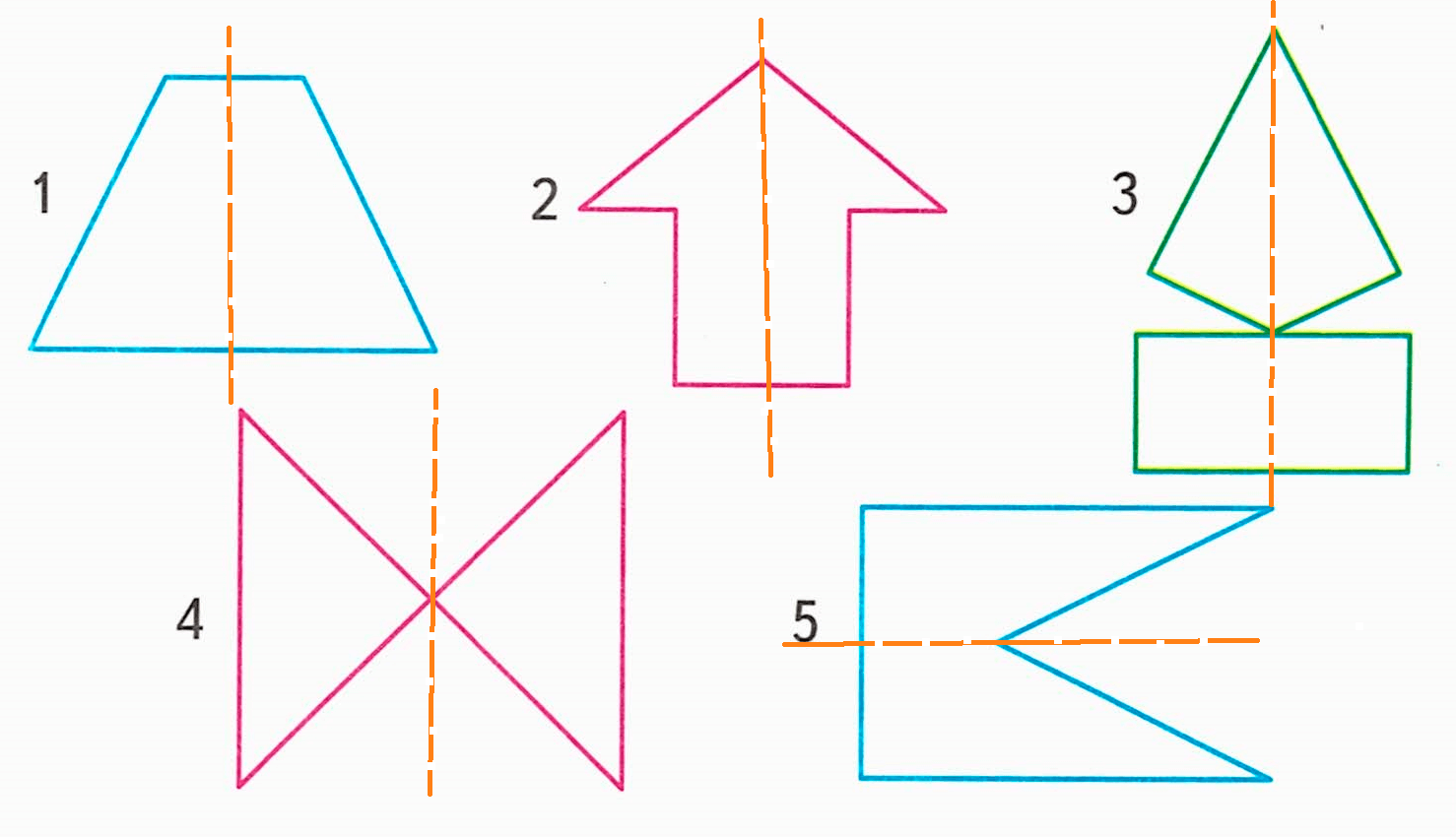
Красным цветом нарисованы оси симметрии.

2) Начертим на листе клетчатой бумаги такой квадрат и разрежем его по указанным линиям:
3) Рассмотрим фигуры:
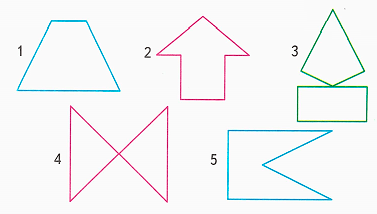
4) Запишем номера фигур, которые можно выложить, используя полученные части квадрата:
1), 3), 5).
5) Подумаем, чему равна площадь каждой фигуры:
Площадь исходного квадрата равна:
3 • 3 = 9 см²;
Так как все составленные фигуры составлены из этого квадрата, значит, что площадь каждой из этих фигур будет тоже равна 9 см².
6) Подумаем, верно ли, что все фигуры 1 – 5 будут симметричными:
Да, все фигуры являются симметричными, а значит, утверждение верно.
Краткое условие: Найди по плану на площадь огорода.
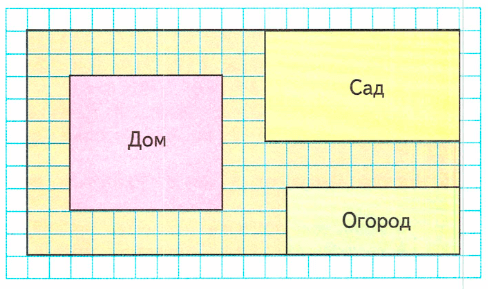
2) Найдём по плану площадь огорода:

1) S = 3 ∙ 8 = 24 м² – площадь огорода
Ответ: площадь огорода равна 24 м².



