3класс
Страница 59, ГДЗ по математике за 3 класс к учебнику Моро часть 1
Номер задания: 1
Краткое условие: На одной полке 4 коробки с большими машинками, по 10 машинок в каждой, а на другой — 50 маленьких машинок. Задай вопрос, нужный для каждого решения:
Решение:
1) Сколько машинок на двух полках всего?
10 ∙ 4 + 50 = 90 (машинок) - всего.
10 ∙ 4 + 50 = 90 (машинок) - всего.
Ответ:
90 машинок.
2) На сколько больших машинок больше, чем маленьких?
50 - 10 ∙ 4 = на 10 (машинок) - больше больших, чем маленьких.
50 - 10 ∙ 4 = на 10 (машинок) - больше больших, чем маленьких.
Ответ:
на 10 машинок.
Решение:
Зададим вопрос, нужный для каждого решения:
1) 10 • 4 + 50;
На одной полке 4 коробки с большими машинками, по 10 машинок в каждой, а на другой – 50 маленьких машинок. Сколько всего машинок на двух полках?
2) 50 - 10 • 4;
На одной полке 4 коробки с большими машинками, по 10 машинок в каждой, а на другой – 50 маленьких машинок. На сколько маленьких машинок больше, чем больших?
1) 10 • 4 + 50;
На одной полке 4 коробки с большими машинками, по 10 машинок в каждой, а на другой – 50 маленьких машинок. Сколько всего машинок на двух полках?
2) 50 - 10 • 4;
На одной полке 4 коробки с большими машинками, по 10 машинок в каждой, а на другой – 50 маленьких машинок. На сколько маленьких машинок больше, чем больших?
Номер задания: 2
Решение:
9 ∙ 4 = 36;
7 ∙ 8 = 56;
8 ∙ 9 = 72;
56 ÷ 8 ∙ 5 = 7 ∙ 5 = 35;
64 ÷ 8 ∙ 7 = 8 ∙ 7 = 56;
42 ÷ 7 ∙ 8 = 6 ∙ 8 = 48;
91 - (6 + 85) = 91 - 91 = 0;
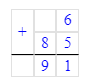
55 + 8- 29 = 63 - 29 = 34;
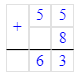
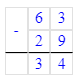
41 - 5 + 36 = 36 + 36 = 72;
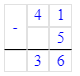
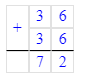
6 ∙ 3 = 18;
1 ∙ 3 = 3;
0 ∙ 3 = 0.
7 ∙ 8 = 56;
8 ∙ 9 = 72;
56 ÷ 8 ∙ 5 = 7 ∙ 5 = 35;
64 ÷ 8 ∙ 7 = 8 ∙ 7 = 56;
42 ÷ 7 ∙ 8 = 6 ∙ 8 = 48;
91 - (6 + 85) = 91 - 91 = 0;

55 + 8- 29 = 63 - 29 = 34;


41 - 5 + 36 = 36 + 36 = 72;


6 ∙ 3 = 18;
1 ∙ 3 = 3;
0 ∙ 3 = 0.
Чтобы вычислить значение выражения, надо сначала определить порядок действий. Все действия выполняются слева направо по порядку.
ШАГ 1. Выполняем действия в скобках.
ШАГ 2. Выполняем умножение и деление по порядку.
ШАГ 3. Выполняем сложение и вычитание по порядку.
ШАГ 1. Выполняем действия в скобках.
ШАГ 2. Выполняем умножение и деление по порядку.
ШАГ 3. Выполняем сложение и вычитание по порядку.
Решение:
1) 9 • 4 = 36;
2) 7 • 8 = 56;
3) 8 • 9 = 72;
11) 1 • 3 = 3;
12) 0 • 3 = 0;
2) 7 • 8 = 56;
3) 8 • 9 = 72;
4) 56 : 8 • 5 = 35;
56 : 8 = 7;
7 • 5 = 35;
5) 64 : 8 • 7 = 56;
64 : 8 = 8;
8 • 7 = 56;
6) 42 : 7 • 8 = 48;
42 : 7 = 6;
6 • 8 = 48;
7) 91 - (6 + 85) = 0;
6 + 85 = 91;


91 - 91 = 0;
8) 55 + 8 - 29 = 34;
55 + 8 = 63;


63 - 29 = 34;


9) 41 - 5 + 36 = 72;
10) 6 • 3 = 18;41 - 5 = 36;


36 + 36 = 72;


11) 1 • 3 = 3;
12) 0 • 3 = 0;
Ответ:
1) 36; 2) 56; 3) 72; 4) 35; 5) 56; 6) 48; 7) 0; 8) 34; 9) 72; 10) 18; 11) 3; 12) 0.
Номер задания: 3
Краткое условие: Заполни таблицу и проследи, как при одном и том же делимом менялся делитель и как — частное.
Решение:

Решение:
1) Рассмотрим таблицу:
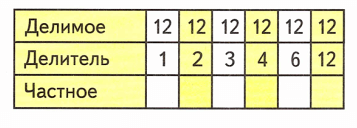
2) Заполним таблицу:
1. 12 : 1 = 12;
2. 12 : 2 = 6;
3. 12 : 3 = 4;
4. 12 : 4 = 3;
5. 12 : 6 = 2;
6. 12 : 12 = 1;
Следовательно, начальная таблица примет следующий вид:
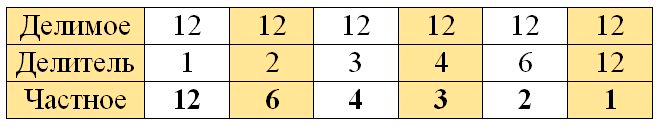
3) Подумаем, как при одном и том же делимом менялся делитель и как - частное:
Чем больше делитель – тем меньше частное, а чем меньше делитель – тем больше частное.

2) Заполним таблицу:
1. 12 : 1 = 12;
2. 12 : 2 = 6;
3. 12 : 3 = 4;
4. 12 : 4 = 3;
5. 12 : 6 = 2;
6. 12 : 12 = 1;
Следовательно, начальная таблица примет следующий вид:
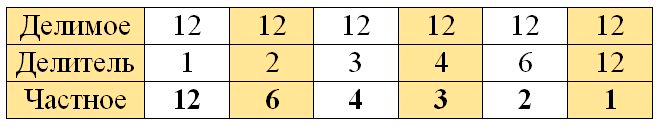
3) Подумаем, как при одном и том же делимом менялся делитель и как - частное:
Чем больше делитель – тем меньше частное, а чем меньше делитель – тем больше частное.
Номер задания: 4
Краткое условие: Чем похожи и чем различаются задачи и их решения?
1)
Дано:

Решение:
1) 80 ÷ 8 = 10 (р.) - цена 1 набора бумаги;
1) 10 ∙ 5 = 50 (р.) - стоят 5 наборов цветной бумаги.
1) 10 ∙ 5 = 50 (р.) - стоят 5 наборов цветной бумаги.
Ответ:
50 рублей.
2)
Дано:

Решение:
1) 80 ÷ 8 = 10 (р.) - цена 1 набора бумаги;
2) 60 ÷ 10 = 6 (шт.) - наборов цветной бумаги стоят 60 рублей.
2) 60 ÷ 10 = 6 (шт.) - наборов цветной бумаги стоят 60 рублей.
Ответ:
6 наборов.
В двух задачах известна общая стоимость определённого количества наборов. В первом действии находим цену.
Различие в решении, во втором действии. В первой задаче находим стоимость другого количества наборов, а во второй находим количество наборов.
Различие в решении, во втором действии. В первой задаче находим стоимость другого количества наборов, а во второй находим количество наборов.
1) Решим задачи:
1.
1.
Дано:
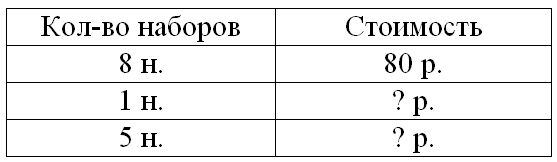
Решение:
Шаг 1. Найдём стоимость 1 набора:
1) 80 : 8 = 10 р. – цена 1 набора
Шаг 2. Найдём стоимость 5 таких наборов:
2) 10 • 5 = 50 р. – цена 5 наборов
1) 80 : 8 = 10 р. – цена 1 набора
Шаг 2. Найдём стоимость 5 таких наборов:
2) 10 • 5 = 50 р. – цена 5 наборов
Ответ:
цена 5 наборов равна 50 рублям.
2.
Дано:

Решение:
Шаг 1. Найдём стоимость 1 набора:
1) 80 : 8 = 10 р. – цена 1 набора
Шаг 2. Найдём сколько таких наборов можно купить на 60 рублей:
2) 60 : 10 = 6 н. – столько наборов можно купить
1) 80 : 8 = 10 р. – цена 1 набора
Шаг 2. Найдём сколько таких наборов можно купить на 60 рублей:
2) 60 : 10 = 6 н. – столько наборов можно купить
Ответ:
на 60 рублей можно купить 6 наборов цветной бумаги.
2) Подумаем, чем похожи задачи:
Задачи похожи тем, что и в первой, и во второй задаче в первом действии необходимо узнать цену одного набора.
3) Подумаем, чем различаются задачи:
В первой задаче необходимо узнать стоимость с помощью умножения, а во второй задаче – количество с помощью деления.
Задачи похожи тем, что и в первой, и во второй задаче в первом действии необходимо узнать цену одного набора.
3) Подумаем, чем различаются задачи:
В первой задаче необходимо узнать стоимость с помощью умножения, а во второй задаче – количество с помощью деления.
Номер задания: 5
Решение:
26 - 6 - 7 = 13;
7 + 9 + 2 = 18;
9 + 9 + 2 = 20;
9 ∙ 2 - 2 = 16;
2 ∙ 2 - 4 = 0;
8 ∙ 9 - 2 = 70;
8 ∙ 4 - 2 = 30;
40 ÷ 5 ∙ 7 = 56.
7 + 9 + 2 = 18;
9 + 9 + 2 = 20;
9 ∙ 2 - 2 = 16;
2 ∙ 2 - 4 = 0;
8 ∙ 9 - 2 = 70;
8 ∙ 4 - 2 = 30;
40 ÷ 5 ∙ 7 = 56.
Решение:
1) 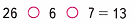
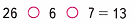
26 – 6 – 7 = 20 – 7 = 13;
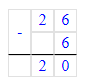
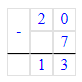
2) 

7 + 9 + 2 = 16 + 2 = 18;
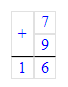
3) 

9 + 9 + 2 = 18 + 2 = 20;
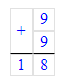
4) 

9 • 2 - 2 = 18 - 2 = 16;
5) 

2 • 2 – 4 = 4 – 4 = 0;
6) 

8 • 9 – 2 = 72 – 2 = 70;
7) 

8 • 4 – 2 = 32 – 2 = 30;
8) 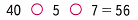
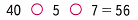
40 : 5 • 7 = 8 • 7 = 56;
Номер задания: 6
Краткое условие: В каком уравнении каждой пары значение х будет больше? Сколькими способами это можно узнать? Какой способ выбираешь ты?
Решение:
x + 34 = 68
x + 38 = 68
В первом уравнении значение x будет больше, потому что второе слагаемое меньше, а значение суммы одинаковое.
96 - x = 15
96 - x = 18
В первом уравнении значение x будет больше, потому что разность меньше.
x - 29 = 60
x - 39 = 60
В первом уравнении значение x будет больше, потому что вычитаемое меньше, а значение разности одинаковое.
x + 38 = 68
В первом уравнении значение x будет больше, потому что второе слагаемое меньше, а значение суммы одинаковое.
96 - x = 15
96 - x = 18
В первом уравнении значение x будет больше, потому что разность меньше.
x - 29 = 60
x - 39 = 60
В первом уравнении значение x будет больше, потому что вычитаемое меньше, а значение разности одинаковое.
Решение:
1) Рассмотрим уравнения:
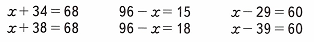
2) Подумаем, сколькими способами можно узнать, в каком уравнении каждой пары значение х будет больше:
Можно это узнать 2 способами: сравнением самих уравнений и сравнением ответов после решения уравнений.
3) Подумаем, в каком уравнении каждой пары значение х будет больше:
1. При одинаковых суммах первое слагаемое будет больше в том уравнении, в котором меньше второе слагаемое.
Значение х в первой паре будет больше в уравнении x + 34 = 68, так как 38 – 34 = 4;
2. При одинаковых уменьшаемых вычитаемое будет больше в том уравнении, в котором меньше разность.
Значение х во второй паре будет больше в уравнении 96 – x = 15, так как 18 – 15 = 3;
3. При одинаковых разностях уменьшаемое будет больше в том уравнении, в котором меньше вычитаемое.
Значение х в третьей паре будет больше в уравнении x – 29 = 60, так как 39 – 29 = 10;
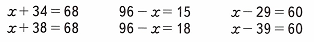
2) Подумаем, сколькими способами можно узнать, в каком уравнении каждой пары значение х будет больше:
Можно это узнать 2 способами: сравнением самих уравнений и сравнением ответов после решения уравнений.
3) Подумаем, в каком уравнении каждой пары значение х будет больше:
1. При одинаковых суммах первое слагаемое будет больше в том уравнении, в котором меньше второе слагаемое.
Значение х в первой паре будет больше в уравнении x + 34 = 68, так как 38 – 34 = 4;
2. При одинаковых уменьшаемых вычитаемое будет больше в том уравнении, в котором меньше разность.
Значение х во второй паре будет больше в уравнении 96 – x = 15, так как 18 – 15 = 3;
3. При одинаковых разностях уменьшаемое будет больше в том уравнении, в котором меньше вычитаемое.
Значение х в третьей паре будет больше в уравнении x – 29 = 60, так как 39 – 29 = 10;
Номер задания: Задача на полях
Решение:
1) 24 : 8 = 3;
2) 56 : 7 = 8;
3) 6 • 8 = 48;
4) 8 • 4 = 32;
2) 56 : 7 = 8;
3) 6 • 8 = 48;
4) 8 • 4 = 32;
Ответ:
1) 3; 2) 8; 3) 48; 4) 32.
Номер задания: Цепочка
Решение:
1) Рассмотрим цепочку вычислений:
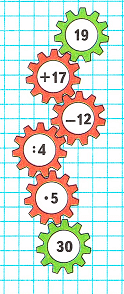
2) Разгадаем цепочку вычислений:
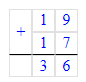
1. 19 + 17 = 36;
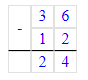
2. 36 - 12 = 24;
3. 24 : 4 = 6;
4. 6 • 5 = 30;

2) Разгадаем цепочку вычислений:
1. 19 + 17 = 36;

2. 36 - 12 = 24;

3. 24 : 4 = 6;
4. 6 • 5 = 30;
Ответ:
30.



