Страница 49, ГДЗ по математике за 3 класс к учебнику Моро часть 1
Краткое условие: Чем задачи 1) и 2) похожи? Чем различаются? Можно ли утверждать, что решения этих задач будут разными? Реши задачи.
1)
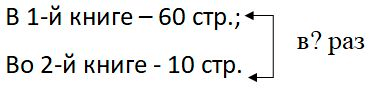
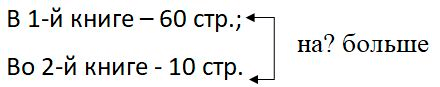
Да, решения задач будут разными, так как у них разные вопросы.
2) Решим задачи:
1.
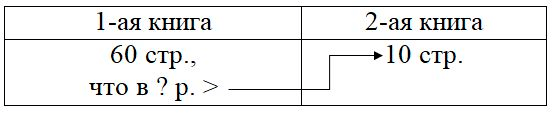
1) 60 : 10 = 6 р. – во столько раз больше

1) 60 - 10 = 50 стр. – на столько страниц больше
Обе задачи связаны с разностным сравнением количества страниц в двух книгах.
4) Подумаем, чем различаются задачи:
В первой задаче необходимо найти во сколько раз в первой книге страниц больше, чем во второй. Во второй задаче нужно найти на сколько страниц больше.

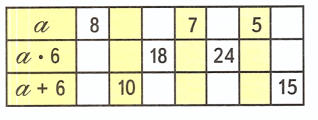
2) Заполним таблицу:
1. Если а = 8, то а • 6 = 8 • 6 = 48;
2. Если а = 8, то а + 6 = 8 + 6 = 14;

3. Если а + 6 = 10, то а = 10 – 6 = 4;
4. Если а = 4, то а • 6 = 4 • 6 = 24;
5. Если а • 6 = 18, то а = 18 : 6 = 3;
6. Если а = 3, то а + 6 = 3 + 6 = 9;
7. Если а = 7, то а • 6 = 7 • 6 = 42;
8. Если а = 7, то а + 6 = 7 + 6 = 13;

9. Если а • 6 = 24, то а = 24 : 6 = 4;
10. Если а = 4, то а + 6 = 4 + 6 = 10;
11. Если а = 5, то а • 6 = 5 • 6 = 30;
12. Если а = 5, то а + 6 = 5 + 6 = 11;
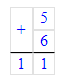
13. Если а + 6 = 15, то а = 15 – 6 = 9;
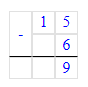
14. Если а = 9, то а • 6 = 9 • 6 = 54;
Следовательно, начальная таблица примет следующий вид:
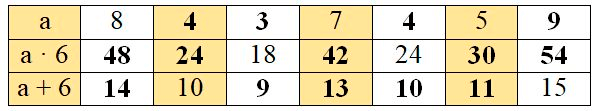
Краткое условие: 1) Начерти прямоугольник, длины сторон которого 6 см и 2 см, и найди его периметр. 2) Начерти другой прямоугольник, периметр которого равен периметру начерченного прямо-угольника, а длина одной из сторон равна 3 см.
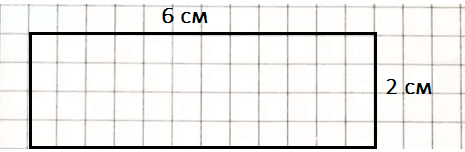
Периметр прямоугольника: (6 + 2) ∙ 2 = 16 см.
2)
Если периметр прямоугольника равен 16 см , а одна сторона 3 см, то вторая сторона равна: 16 ÷ 2 - 3 = 5 см.
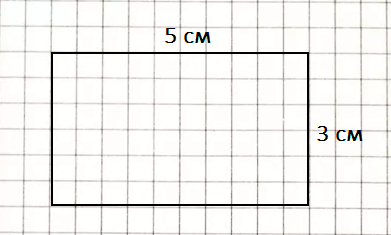
2) Найдем периметр данного прямоугольника:
Р = (6 + 2) • 2 = 8 • 2 = 16 (см);
3) Начертим другой прямоугольник, периметр которого равен периметру начерченного прямоугольника, а длина одной из сторон равна 3 см:
Если длина одной из сторон равна 3 см, то длина другой стороны равна:
16 : 2 – 3 = 8 – 3 = 5 (см);
Следовательно, длины сторон другого прямоугольника равны 3 см и 5 см.
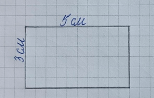
Краткое условие: Собрали 18 кг вишни. Из них взяли на компот 3 кг вишни, а на варенье в 4 раза больше, чем на компот. Составь различные выражения и объясни, что они обозначают.

1) 3 • 4;
(данное выражение обозначает сколько взяли вишни на варенье)
2) 3 • 4 + 3;
(данное выражение обозначает сколько всего вишен пошло на варенье и компот вместе)
3) 3 • 4 - 3;
(данное выражение обозначает на сколько больше вишен взяли на варенье, чем на компот)
4) 18 – (3 • 4 + 3);
(данное выражение обозначает сколько вишни осталось после приготовления компота и варенья)
Краткое условие: Тетрадь стоит 8 р., а книга — в 4 раза дороже, чем тетрадь. На сколько рублей тетрадь дешевле, чем книга?
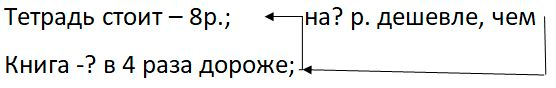
2) 32 - 8 = на 24 (р.) - тетрадь дешевле книги.
ШАГ 1. Найти стоимость книги.
ШАГ 2. Найти на сколько рублей тетрадь дешевле, чем книга.

1) 8 • 4 = 32 р. – стоимость книги
Шаг 2. Найдём на сколько рублей тетрадь дешевле, чем книга:
2) 32 - 8 = 24 р. – на столько дешевле
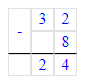
2) 32 - 8 = 24 (р.)
Ответ: тетрадь дешевле книги на 24 рубля.
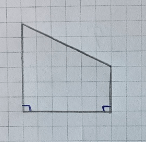
Краткое условие: Начерти четырёхугольник, в котором 2 прямых угла, один тупой и один острый угол.
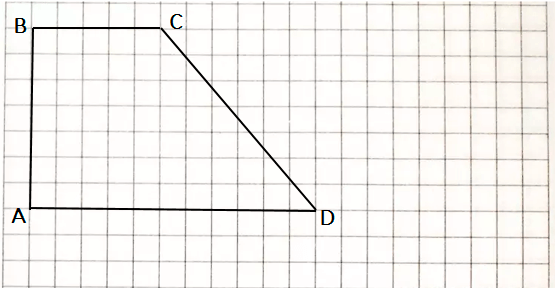
Прямые углы: DAB, ABC.
Тупой угол: BCD.
Острый угол: CDA.
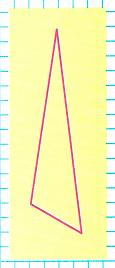
Краткое условие: Из куска проволоки сначала сделали треугольник, как на рисунке, а затем пятиугольник с равными сторонами. Найди длину стороны пятиугольника.
Для того, чтобы построить треугольник взяли проволоку длиной 15 см.
По условию задачи у пятиугольника все стороны равны, значит 15 см ÷ 5 = 3 см - каждая сторона пятиугольника.
ШАГ 1. Найти периметр треугольника.
ШАГ 2. Найти длину стороны пятиугольника.
2) Решим задачу:

1) Р = 2 см + 6 см + 7 см = 8 см + 7 см = 15 см – периметр треугольника

Шаг 2. Найдём длину стороны пятиугольника:
2) 15 : 5 = 3 см – длина стороны пятиугольника
2) 15 ∶ 5 = 3 (см)
Ответ: длина стороны пятиугольника равна 3 см.
Краткое условие: Мальчик вошёл в лифт на третьем этаже и, проехав 2 этажа, вышел из лифта. На каком этаже мальчик мог выйти из лифта?
Если мальчик поехал вниз, то 3 - 2 = 1 этаж.
1) Если мальчик ехал вверх, то 3 + 2 = 5;
Следовательно, он мог выйти на 5 этаже.
2) Если мальчик ехал вниз, то 3 - 2 = 1;
Следовательно, он мог выйти на 1 этаже.



