3класс
Страница 16, ГДЗ по математике за 3 класс к учебнику Моро часть 1
Номер задания: 17
Краткое условие: 1) Найди периметр каждого треугольника в миллиметрах. 2) Назови прямые, острые и тупые углы в этих треугольниках.
Решение:
1)
Периметр треугольника АВС: 17 мм + 20 мм + 35 мм = 72 мм;
Периметр треугольника KLM: 30 мм + 25 мм + 40 мм = 95 мм;
Периметр треугольника EFN: 30 мм + 30 мм + 30 мм = 90 мм.
2)
Прямой угол только в треугольнике KLM – это угол KLM.
Острые углы:
Угол ВАС, угол ВСА в треугольнике АВС.
Угол LKM, угол LMK в треугольнике KLM.
Угол FEN, угол ENF, угол EFN в треугольнике EFN.
Тупой угол только в треугольнике АВС – это угол АВС.
Периметр треугольника АВС: 17 мм + 20 мм + 35 мм = 72 мм;
Периметр треугольника KLM: 30 мм + 25 мм + 40 мм = 95 мм;
Периметр треугольника EFN: 30 мм + 30 мм + 30 мм = 90 мм.
2)
Прямой угол только в треугольнике KLM – это угол KLM.
Острые углы:
Угол ВАС, угол ВСА в треугольнике АВС.
Угол LKM, угол LMK в треугольнике KLM.
Угол FEN, угол ENF, угол EFN в треугольнике EFN.
Тупой угол только в треугольнике АВС – это угол АВС.
Решение:
1) Рассмотрим чертёж:
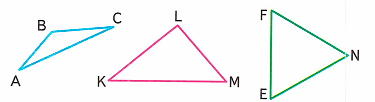
2) Найдем периметр каждого треугольника в миллиметрах:
1. Р = АВ + ВС + АС = 17 мм + 21 мм + 35 мм = 38 мм + 35 мм = 73 мм;
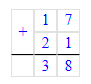
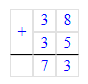
2. Р = КL + LM + КМ = 30 мм + 25 мм + 40 мм = 70 мм + 25 мм = 95 мм;
3. Р = ЕF + FN + ЕN = 30 мм + 30 мм + 30 мм = 60 мм + 30 мм = 90 мм;
3) Назовем прямые, острые и тупые углы в этих треугольниках:
1. ∆АВС;
∠ВАС – острый угол;
∠АВС – тупой угол;
∠ВСА – острый угол;
2. ∆КLM;
∠КLM – прямой угол;
∠LMК – острый угол;
∠МКL – острый угол;
3. ∆FNЕ;
∠FNЕ – острый угол;
∠NЕF – острый угол;
∠ЕFN – острый угол;

2) Найдем периметр каждого треугольника в миллиметрах:
1. Р = АВ + ВС + АС = 17 мм + 21 мм + 35 мм = 38 мм + 35 мм = 73 мм;


2. Р = КL + LM + КМ = 30 мм + 25 мм + 40 мм = 70 мм + 25 мм = 95 мм;
3. Р = ЕF + FN + ЕN = 30 мм + 30 мм + 30 мм = 60 мм + 30 мм = 90 мм;
3) Назовем прямые, острые и тупые углы в этих треугольниках:
1. ∆АВС;
∠ВАС – острый угол;
∠АВС – тупой угол;
∠ВСА – острый угол;
2. ∆КLM;
∠КLM – прямой угол;
∠LMК – острый угол;
∠МКL – острый угол;
3. ∆FNЕ;
∠FNЕ – острый угол;
∠NЕF – острый угол;
∠ЕFN – острый угол;
Номер задания: 18
Краткое условие: Начерти два прямоугольника: 2×3 см и 2×6 см. На сколько сантиметров их периметры отличаются?
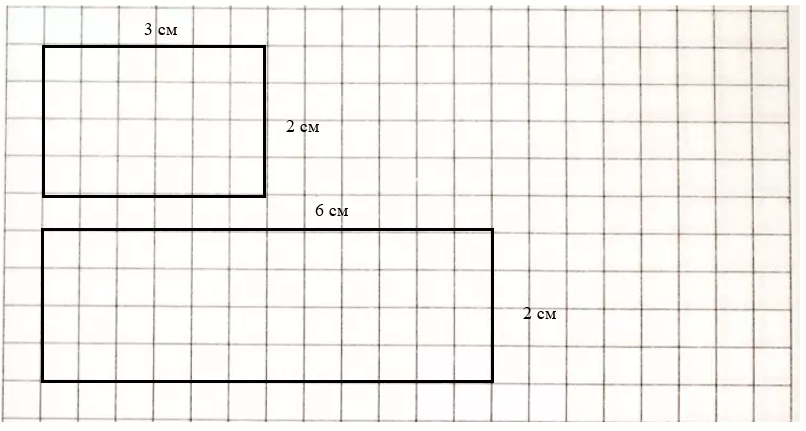
На сколько сантиметров периметр одного из них больше периметра другого?
Решение:
1) (3 + 2) ∙ 2 = 5 ∙ 2 = 10 (см) - периметр первого прямоугольника;
2) (6 + 2) ∙ 2 = 8 ∙ 2 = 16 (см) - периметр второго прямоугольника;
3) 16 - 10 = на 6 (см) - периметр прямоугольника со сторонами 2 см и 6 см больше периметра прямоугольника со сторонами 2 см и 3 см.
2) (6 + 2) ∙ 2 = 8 ∙ 2 = 16 (см) - периметр второго прямоугольника;
3) 16 - 10 = на 6 (см) - периметр прямоугольника со сторонами 2 см и 6 см больше периметра прямоугольника со сторонами 2 см и 3 см.
Ответ:
на 6 см больше.
Решение:
1) Начертим прямоугольник со сторонами 2 см и 3 см:

2) Начертим прямоугольник со сторонами 2 см и 6 см:

3) Вычислим периметр первого прямоугольника:
Р = 2 см + 3 см + 2 см + 3 см = 5 см + 5 см = 10 см;
4) Вычислим периметр второго прямоугольника:
Р = 2 см + 6 см + 2 см + 6 см = 8 см + 8 см = 16 см;
5) Подумаем, на сколько сантиметров периметр одного прямоугольника больше периметра другого:
16 см – 10 см = 6 см;

2) Начертим прямоугольник со сторонами 2 см и 6 см:

3) Вычислим периметр первого прямоугольника:
Р = 2 см + 3 см + 2 см + 3 см = 5 см + 5 см = 10 см;
4) Вычислим периметр второго прямоугольника:
Р = 2 см + 6 см + 2 см + 6 см = 8 см + 8 см = 16 см;

5) Подумаем, на сколько сантиметров периметр одного прямоугольника больше периметра другого:
16 см – 10 см = 6 см;
Ответ:
на 6 см больше.
Номер задания: 19
Краткое условие: На двух аллеях по b клёнов, остальные — на третьей. Всего 19 клёнов.
1 способ:
Дано:
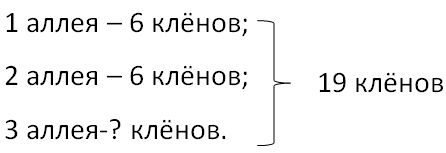
Решение:
1) 19 - 6 = 13 (кл.) - на 2-й и 3-й аллее;
2) 13 - 6 = 7 (кл.) - на 3-й аллее.
2) 13 - 6 = 7 (кл.) - на 3-й аллее.
Ответ:
7 клёнов на 3-й аллее.
2 способ:
Дано:
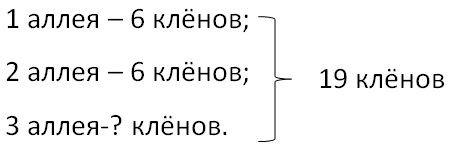
Решение:
1) 6 ∙ 2 = 12 (кл.) - на 1-й и 2-й аллее вместе;
2) 19 - 12 = 7 (кл.) - на 3-й аллее.
2) 19 - 12 = 7 (кл.) - на 3-й аллее.
Ответ:
7 клёнов на 3-й аллее.
Оба решения верные. В 1-м способе по очереди вычитают количество клёнов от общего количества. Во 2-м способе сначала находят количество клёнов на 1-й и 2-й аллее вместе, а потом вычитают из общего количества.
Решение:
1) Рассмотрим решения задач:
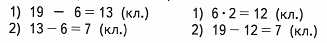
2) Объясним, почему верно каждое решение:
1 решение:
Сначала узнали сколько клёнов высадили на второй и третьей аллее вместе с помощью вычитания, а после сколько клёнов высадили на третьей аллее с помощью вычитания.
2 решение:
Сначала узнали сколько клёнов высадили на первой и второй аллее с помощью умножения, а после сколько клёнов высадили на третьей аллее с помощью вычитания.
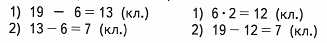
2) Объясним, почему верно каждое решение:
1 решение:
Сначала узнали сколько клёнов высадили на второй и третьей аллее вместе с помощью вычитания, а после сколько клёнов высадили на третьей аллее с помощью вычитания.
2 решение:
Сначала узнали сколько клёнов высадили на первой и второй аллее с помощью умножения, а после сколько клёнов высадили на третьей аллее с помощью вычитания.
Номер задания: 20
Краткое условие: Снимай верхний треугольник, записывай его число. Продолжай, пока не снимешь все. Определи правило ряда и запиши следующие три числа.
Решение:

Решение:
1) Рассмотрим рисунок:
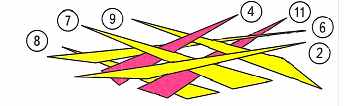
2) Найдем треугольник, лежащий сверху, и «снимем» его, запишем число, на которое он показывает. Таким образом снимем все треугольники, образовав ряд чисел:
2; 7; 4; 9; 6; 11; 8;
3) Определим, по какому правилу составлен ряд чисел:
Сначала к числу прибавляется 5 единиц, а потом вычитается 3 единицы. Данный алгоритм справедлив для всего числового ряда.
4) Запишем следующие три числа ряда:
1. 8 + 5 = 13;
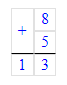
2. 13 – 3 = 10;
3. 10 + 5 = 15;

2) Найдем треугольник, лежащий сверху, и «снимем» его, запишем число, на которое он показывает. Таким образом снимем все треугольники, образовав ряд чисел:
2; 7; 4; 9; 6; 11; 8;
3) Определим, по какому правилу составлен ряд чисел:
Сначала к числу прибавляется 5 единиц, а потом вычитается 3 единицы. Данный алгоритм справедлив для всего числового ряда.
4) Запишем следующие три числа ряда:
1. 8 + 5 = 13;

2. 13 – 3 = 10;
3. 10 + 5 = 15;
Ответ:
13; 10; 15.
Номер задания: 21
Краткое условие: Покажи с помощью сгибания каждой фигуры все её оси симметрии.
Решение:
Решение:
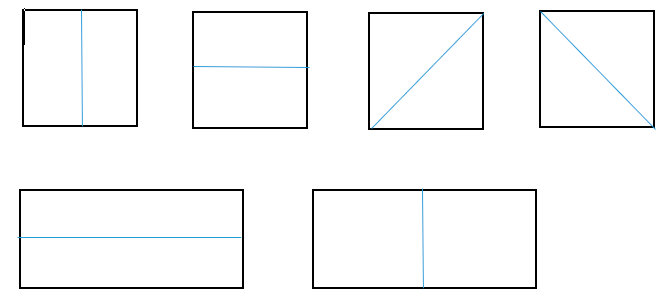
1) Рассмотрим чертёж:
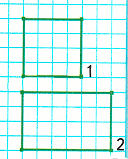
2) Начертим в тетради такие же фигуры, а после вырежем:

После вырезания получился квадрат со сторонами 2 см и прямоугольник со сторонами 2 см и 3 см.
3) С помощью сгибания каждой фигуры покажем все оси симметрии:

Следовательно, у квадрата 4 оси симметрии, а у прямоугольника – 2.

2) Начертим в тетради такие же фигуры, а после вырежем:

После вырезания получился квадрат со сторонами 2 см и прямоугольник со сторонами 2 см и 3 см.
3) С помощью сгибания каждой фигуры покажем все оси симметрии:

Следовательно, у квадрата 4 оси симметрии, а у прямоугольника – 2.
Смотрите ещё задания из учебника:
Страница 10
Страница 11
Страница 12
Страница 13
Страница 14
Страница 19
Страница 20
Страница 21
Страница 22
Страница 23
... смотреть все номера



