Страница 106, ГДЗ по математике за 3 класс к учебнику Моро часть 1
Краткое условие: Из одной третьей части бруска красного пластилина вылепили 4 одинаковые вишенки. Сколько таких вишенок можно вылепить из целого бруска пластилина?
Из целого бруска - ? вишенок.
ШАГ 1. Найти сколько вишенок можно вылепить из целого бруска пластилина.

1) 4 • 3 = 12 в. – из целого бруска пластилина
Ответ: из целого бруска пластилина можно вылепить 12 вишенок.
Краткое условие: Заполни пропуски.
Одна шестая часть суток – это 24 ÷ 6 = 4 ч.
Одна десятая часть часа – это 60 ÷ 10 = 6 мин.
1) Одна четвёртая часть года – это 3 мес.
12 : 4 = 3;
2) Одна шестая часть суток – это 4 ч.
24 : 6 = 4;
3) Одна десятая часть часа – это 6 мин.
60 : 10 = 6;
Краткое условие: Начерти две окружности с одним центром так, чтобы радиус первой был 3 см, а радиус второй составлял третью часть радиуса первой окружности. Закрась круг с меньшим радиусом.
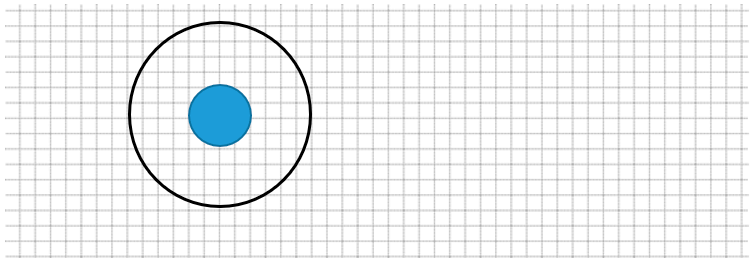
3 : 3 = 1 (см);
Следовательно, радиус второй окружности равен 1 см.
2) Начертим две окружности с одним центром так, чтобы радиус первой был 3 см, а радиус второй – 1 см:
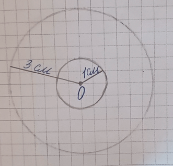
3) Закрасим круг с меньшим радиусом:
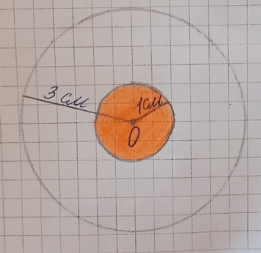
Краткое условие: Скажи, чему равно значение х в каждом из данных уравнений.
x = 0.
48 - x = 0
x = 48.
27 ÷ x = 1;
x = 27.
x ÷ 9 = 0;
x = 0.
62 ∙ x = 62;
x = 1.
74 ÷ x = 1;
x = 74.
х = 36 – 36;
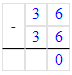
х = 0;
2) 48 – х = 0;
х = 48 – 0;
х = 48;
3) 27 : х = 1;
х = 27 : 1;
х = 27;
4) х : 9 = 0;
х = 0 ∙ 9;
х = 0;
5) 62 • х = 62;
х = 62 : 62;
х = 1;
6) 74 : х = 1;
х = 74 : 1;
х = 74;
Краткое условие: На конкурсе «Смекалка» за решение каждой задачи давалось 6 очков, за решение примера — 2 очка. Миша решил 3 задачи и 5 примеров. Сколько очков он набрал?
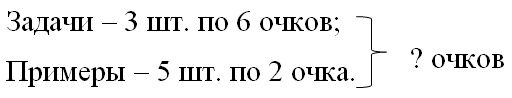
2) 5 ∙ 2 = 10 (очков) - Миша получил за примеры;
3) 18 + 10 = 28 (очков) - получил Миша.
ШАГ 1. Найти сколько очков набрал Миша за решение задач.
ШАГ 2. Найти сколько очков набрал Миша за решение примеров.
ШАГ 3. Найти сколько всего очков набрал Миша.

1) 3 • 6 = 18 очк. – за задачи
Шаг 2. Найдём сколько очков набрал Миша за решение примеров:
2) 2 • 5 = 10 очк. – за примеры
Шаг 3. Найдём сколько всего очков набрал Миша:
3) 18 + 10 = 28 очк. – всего
2) 2 • 5 = 10 (очк.)
3) 18 + 10 = 28 (очк.)
Ответ: Миша набрал 28 очков.
Краткое условие: Назови закрашенные доли круга в порядке их увеличения и в соответствии с этим запиши буквы. Ты получишь зашифрованное слово.
В порядке увеличения: З – одна шестнадцатая; Е – одна двенадцатая; Р – одна восьмая; К – одна шестая; А – одна четвёртая; Л – одна третья; О – одна вторая.
Зашифрованное слово: зеркало.
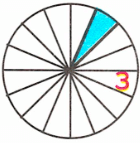
Закрашена одна шестнадцатая доля, значит, первая буква слова - з;
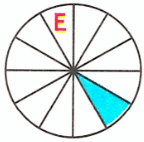
Закрашена одна двенадцатая доля, значит, вторая буква слова - е;
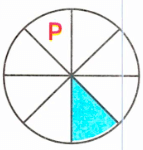
Закрашена одна восьмая доля, значит, третья буква слова - р;
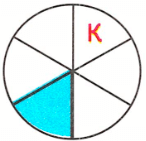
Закрашена одна шестая доля, значит, четвёртая буква слова - к;
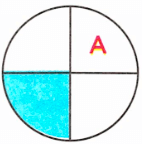
Закрашена одна четвёртая доля, значит, пятая буква слова - а;
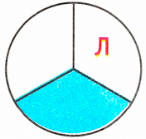
Закрашена одна третья доля, значит, шестая буква слова - л;
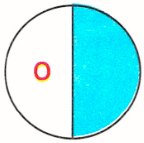
Закрашена одна вторая доля, значит, седьмая буква слова - о;
Следовательно, зашифрованное слово: зеркало.
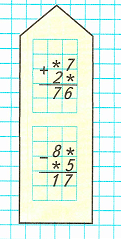
2) Разгадаем ребусы:
1)
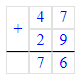
1. Разность чисел 16 и 7 равняется 9. Значит, на месте единиц во втором слагаемом необходимо писать цифру 9.
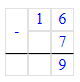
2. Разность чисел 7 и 2 равняется 5, а разность чисел 5 и 1 равняется 4. Значит, на месте десятков в первом слагаемом необходимо писать цифру 4.
Следовательно, начальный ребус примет следующий вид:
47 + 29 = 76;
2)
1. Сумма чисел 5 и 7 равняется 12. 12 единиц – это 1 десяток и 2 единицы. Значит, на месте единиц в уменьшаемом необходимо писать цифру 2.

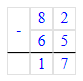
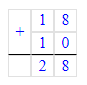
2. Разность чисел 8 и 1 равняется 7. Разность чисел 7 и 1 равняется 6. Значит, на месте десятков в вычитаемом необходимо писать цифру 6.
Следовательно, начальный ребус примет следующий вид:
82 – 65 = 17;