Страница 103, ГДЗ по математике за 3 класс к учебнику Моро часть 1
Краткое условие: Какие числа пропущены?
70 - 35 - 10 = 25;
7 ∙ 2 ∙ 2 ÷ 4 = 7;
(6 + 92) ÷ 1 = 98;
(36 + 14) ∙ 0 = 0;
8 ∙ 6 ÷ 48 = 1.
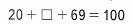
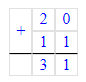
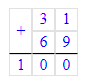
20 + 11 + 69 = 31 + 69 = 100;
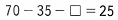
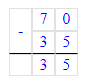
70 – 35 – 10 = 35 – 10 = 25;
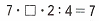
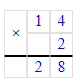
7 • 2 • 2 : 4 = 14 • 2 : 4 = 28 : 4 = 7;
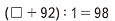
(6 + 92) : 1 = 98 : 1 = 98;
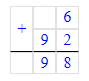
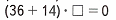
(36 + 14) • 0 = 0;
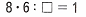
8 • 6 : 48 = 48 : 48 = 1;
Краткое условие: В свободных клетках квадрата 1 размести ещё числа 3, 4, 5, б, 9 так, чтобы получить магический квадрат.

Сумма = 21.
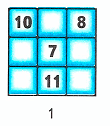
2) В свободных клетках квадрата разместим числа 3, 4, 5, 6, 9 так, чтобы получился магический квадрат:
1. Анализируя уже имеющиеся числа в квадрате, допустим, сумма рядов, столбцов и диагонали равна 21. Тогда в первый ряд необходимо вставить число 3:
10 + 3 + 8 = 13 + 8 = 21;
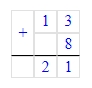
2. Найдем недостающее число диагонали:
21 – (10 + 7) = 21 – 17 = 4;
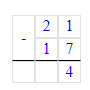
3. Найдем недостающее число третьего ряда:
21 – (11 + 4) = 21 – 15 = 6;
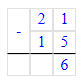
4. Найдем недостающее число первого столбца:
21 – (10 + 6) = 21 – 16 = 5;
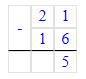
5. Найдем недостающее число второго ряда:
21 – (5 + 7) = 21 – 12 = 9;

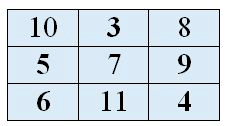
Следовательно, начальный квадрат примет следующий вид:
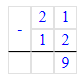
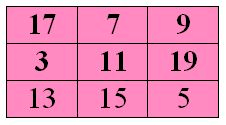
Краткое условие: Оставляя на местах числа 13, 15 и 5 в квадрате 2, расставь в его пустые клетки числа 3, 7, 9, 11, 17, 19 так, чтобы получить магический квадрат.

Сумма = 33.

2) Оставляя на местах числа 13, 15 и 5, расставим в пустых клетках числа 3, 7, 9, 11, 17, 19 так, чтобы получился магический квадрат:
1. Найдем сумму третьего ряда:
13 + 15 + 5 = 28 + 5 = 33;
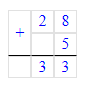
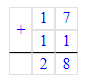
2. Анализируя уже имеющиеся числа в квадрате, допустим, что по диагонали нужно вставить числа 17 и 11, чтобы набрать необходимую сумму:
17 + 11 + 5 = 28 + 5 = 33;
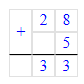
2. Найдем недостающее число второго столбца:
33 – (11 + 15) = 33 – 26 = 7;
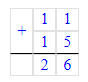
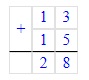
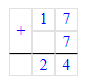
3. Найдем недостающее число первого ряда:
33 – (17 + 7) = 33 – 24 = 9;
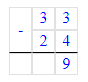
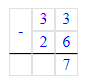
4. Найдем недостающее число третьего столбца:
33 – (9 + 5) = 33 – 14 = 19;

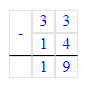
5. Найдем недостающее число первого столбца:
33 – (17 + 13) = 33 – 30 = 3;
Следовательно, начальный квадрат примет следующий вид:
Краткое условие: Используя знаки действий и, если надо, скобки, запиши число 10 четырьмя тройками.
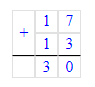
3 ∙ 3 + 3 ÷ 3 = 10;
(33 - 3) ÷ 3 = 10.
3 • 3 + 3 : 3 = 9 + 1 = 10;
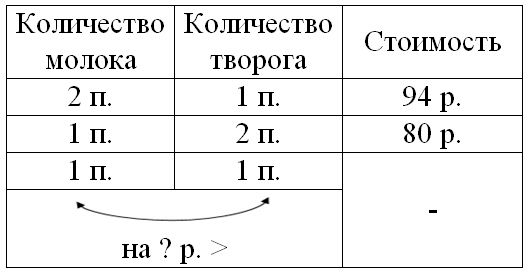
Краткое условие: Два одинаковых пакета молока и пачка творога стоят 94 р. Две такие же пачки творога и один такой же пакет молока стоят 80 р. На сколько рублей один пакет молока дороже одной пачки творога?
Тогда если М + М + Т = 94 р., а Т + Т + М = 80 р., то заметим, что разница в одном пакете молока и пачке творога.
94 - 80 = 14 (р.) - разница больше там, где 2 пакета М, значит молоко дороже.
ШАГ 1. Найти на сколько рублей один пакет молока дороже одной пачки творога.
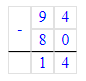
Шаг 1. Найдём на сколько рублей один пакет молока дороже одной пачки творога:
1) 94 - 80 = 14 р. – на столько дороже
Ответ: пакет молока на 14 р. дороже пачки творога.
Краткое условие: Начерти прямоугольник с периметром 12 см и с наибольшей площадью.
1 см и 5 см; 2 см и 4 см; 3 см и 3 см.
Найдём наибольшую площадь:
1 ∙ 5 = 5 см²
2 ∙ 4 = 6 см²
3 ∙ 3 = 9 см²
5 см² < 6 см² < 9 см²
Значит, наибольшая площадь у прямоугольника со сторонами 3 см и 3 см.
1) Если периметр прямоугольника равен 12 см, то стороны прямоугольника могут быть равны:
1. 1 см и 5 см;
2. 2 см и 4 см;
3. 3 см и 3 см;
2) Подумаем, при каких длинах площадь у прямоугольника будет большей:
1. S = 1 • 5 = 5 (см²);
2. S = 2 • 4 = 8 (см²);
3. S = 3 • 3 = 9 (см²);
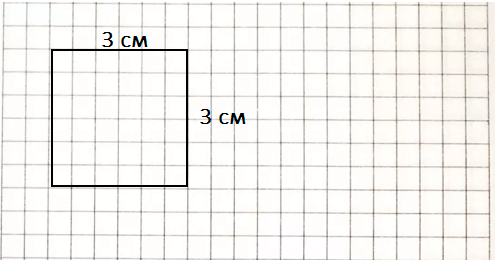
Следовательно, площадь прямоугольника будет большей, если его стороны будут равны 3 см.
3) Начертим данный прямоугольник:
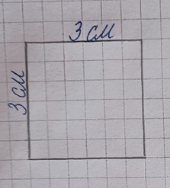
Краткое условие: Ленту разрезали на 3 части, затем одну из этих частей разрезали ещё на 4 части. На сколько всего частей разрезали ленту? Сколько сделали разрезов?
Для того, чтобы разрезать ленту на 3 части, нужно сделать 2 разреза, а чтобы на 4 части 3 разреза.
2) 2 + 3 = 5 (разрезов) - сделали.
2 + 4 = 6;
Значит, ленту разрезали на 6 частей.
2) Подумаем, сколько сделали разрезов:
2 + 3 = 5;
Значит, сделали 5 разрезов.



