Часть 2 страница 30, ГДЗ по математике за 2 класс к учебнику Моро, Бантовой, Бельтюковой Школа России
Страница 30
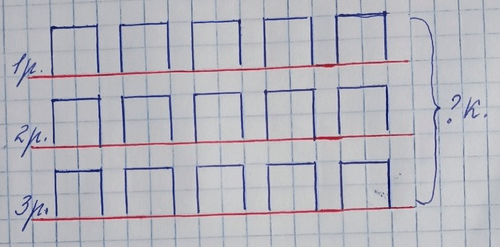
Краткое условие: Объясни, как по-разному подсчитывали общее число кружков в прямоугольниках 1, 2 и 3. Прочитай и запомни вывод.
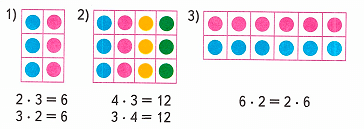
2) Объясним, как по-разному подсчитывали общее число кружков в прямоугольниках:
1 прямоугольник:
1. В первом случае кружочки считали по строкам. В каждой строке по 2 одинаковых кружка. Всего 3 такие строки. Чтобы узнать общее количество кружков, необходимо найти произведение чисел 2 и 3.
2 • 3 = 2 + 2 + 2 = 4 + 2 = 6;
2. Во втором случае кружочки считали по столбцам. В каждом столбце по 3 одинаковых кружка. Всего 2 таких столбца. Чтобы узнать общее количество кружков, необходимо найти произведение чисел 3 и 2.
3 • 2 = 3 + 3 = 6;
2 прямоугольник:
1. В первом случае кружочки считали по строкам. В каждой строке по 4 одинаковых кружка. Всего 3 такие строки. Чтобы узнать общее количество кружков, необходимо найти произведение чисел 4 и 3.
4 • 3 = 4 + 4 + 4 = 8 + 4 = 12;
2. Во втором случае кружочки считали по столбцам. В каждом столбце по 3 одинаковых кружка. Всего 4 таких столбца. Чтобы узнать общее количество кружков, необходимо найти произведение чисел 3 и 4.
3 • 4 = 3 + 3 + 3 + 3 = 6 + 6 = 12;
3 прямоугольник:
1. В первом случае кружочки считали по строкам. В каждой строке по 6 одинаковых кружков. Всего 2 такие строки. Чтобы узнать общее количество кружков, необходимо найти произведение чисел 6 и 2.
6 • 2 = 6 + 6 = 12;
2. Во втором случае кружочки считали по столбцам. В каждом столбце по 2 одинаковых кружка. Всего 6 таких столбцов. Чтобы узнать общее количество кружков, необходимо найти произведение чисел 2 и 6.
2 • 6 = 2 + 2 + 2 + 2 + 2 + 2 = 4 + 4 + 4 = 8 + 4 = 12;
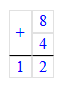
3) Сформулируем вывод:
От перестановки множителей результат умножения не изменяется.
Краткое условие: Используя это свойство умножения, найди значение второго выражения в каждой паре, зная значение первого.
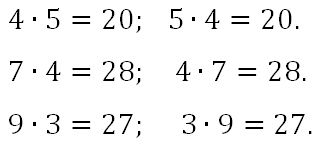
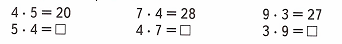
2) Используя свойство умножения, найдем значение второго выражения в каждой паре, зная значение первого:
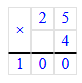
1. 5 ∙ 4 = 4 • 5 = 20;
2. 4 ∙ 7 = 7 ∙ 4 = 28;
3. 3 ∙ 9 = 9 ∙ 3 = 27;
Краткое условие: В школьном саду 3 ряда кустов смородины, по 5 кустов в каждом ряду. Сколько всего кустов смородины в школьном саду? Сделай схематический рисунок и реши задачу.
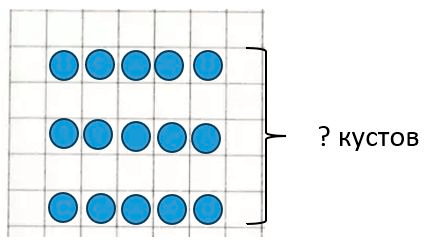
ШАГ 1. Найти сколько всего кустов смородины в школьном саду.
2) Решим задачу:

1) 5 • 3 = 5 + 5 + 5 = 10 + 5 = 15 к. – всего
Ответ: всего в школьном саду 15 кустов смородины.
Краткое условие: Найди периметр квадрата со стороной 25 мм.
Периметр квадрата – ? мм.
ШАГ 1. Найти периметр квадрата.

1) 25 • 4 = 100 мм = 10 см – периметр
Ответ: периметр квадрата равен 10 см.
Краткое условие: На сколько 54 больше.
54 - 19 = на 35 число 54 больше 19;
54 - 36 = на 18 число 54 больше 36;
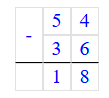
54 - 42 = на 12 число 54 больше 42.
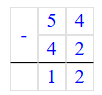
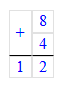
1) 8;
54 – 8 = 46;

Значит, число 54 на 46 единиц больше, чем число 8.
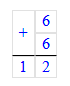
2) 19;
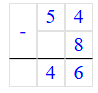
54 – 19 = 35;

Значит, число 54 на 35 единиц больше, чем число 19.
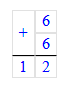
3) 36;
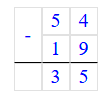
54 – 36 = 18;

Значит, число 54 на 18 единиц больше, чем число 36.
4) 42;
54 – 42 = 12;

Значит, число 54 на 12 единиц больше, чем число 42.
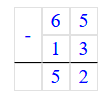
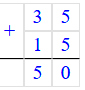
65 + 13 = 78;
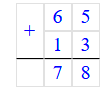
58 + 19 = 77;
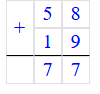
35 + 15 = 50.

2) 65 + 13 = 78;

3) 58 + 19 = 77;

4) 35 + 15 = 50;

Краткое условие: Сколько раз по 3 содержится в числе 6? в числе 9? в числе 12? в числе 15?
В числе 9 содержится 3 раза по 3, потому что 3 ∙ 3 = 9.
В числе 12 содержится 4 раза по 3, потому что 4 ∙ 3 = 12.
В числе 15 содержится 5 раз по 3, потому что 5 ∙ 3 = 15.
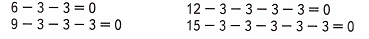
2) Подумаем, сколько раз по три содержится в числах:
1. 6;
Так как 6 – 3 – 3 = 0, это значит, что в числе 6 содержится два раза по три.
2. 9;
Так как 9 – 3 – 3 – 3 = 0, это значит, что в числе 9 содержится три раза по три.
3. 12;
Так как 12 – 3 – 3 – 3 – 3 = 0, это значит, что в числе 12 содержится четыре раза по три.
4. 15;
Так как 15 – 3 – 3 – 3 – 3 – 3 = 0, это значит, что в числе 15 содержится пять раз по три.
Краткое условие: Найди значения выражений.
Если a = 23, то 23 - 7 = 16.
Если a = 57, то 57 - 7 = 50.
Если a = 60, то 60 - 7 = 53.
Если a = 92, то 92 - 7 = 85.
a + 8
Если a = 23, то 23 + 8 = 31.
Если a = 57, то 57 + 8 = 65.
Если a = 60, то 60 + 8 = 68.
Если a = 92, то 92 + 8 = 100.
1. a = 23;
Если a = 23, то a – 7 = 23 – 7 = 16;
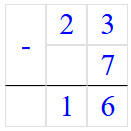
2. a = 57;
Если a = 57, то a – 7 = 57 – 7 = 50;
3. a = 60;
Если a = 60, то a – 7 = 60 – 7 = 53;
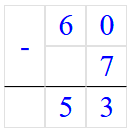
4. a = 92;
Если a = 92, то a – 7 = 92 – 7 = 85;
2) Найдем значения выражения а + 8, если:
1. a = 23;
Если a = 23, то a + 8 = 23 + 8 = 31;

2. а = 57;
Если a = 57, то a + 8 = 57 + 8 = 65;
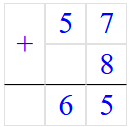
3. а = 60;
Если a = 60, то a + 8 = 60 + 8 = 68;
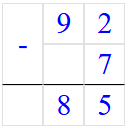
4. а = 92;
Если a = 92, то a + 8 = 92 + 8 = 100;
Краткое условие: Вставь вместо кружка (О) один из этих знаков, чтобы равенство или неравенство стало верным.

От перестановки множителей результат умножения не изменяется.
Поэтому, 7 • 4 = 4 • 7;

Произведение пяти троек больше, чем произведение четырёх троек.
Поэтому, 3 • 5 > 3 • 4;

От перестановки множителей результат умножения не изменяется.
Поэтому, 13 • 2 = 2 • 13;

2) Подумаем, сколько прямоугольников на рисунке:
На чертеже всего 7 прямоугольников.



