Часть 2 страница 28, ГДЗ по математике за 2 класс к учебнику Моро, Бантовой, Бельтюковой Школа России
Страница 28
Краткое условие: Вычисли произведения, заменяя умножение сложением одинаковых слагаемых.
2 ∙ 3 = 2 + 2 + 2 = 6;
1 ∙ 5 = 1 + 1 + 1 + 1 + 1 = 5;
0 ∙ 4 = 0 + 0 + 0 + 0 = 0;
12 ∙ 2 = 12 + 12 = 24.
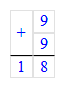
1) 9 ∙ 2 = 9 + 9 = 18;
2) 2 ∙ 3 = 2 + 2 + 2 = 4 + 2 = 6;
3) 1 ∙ 5 = 1 + 1 + 1 + 1 + 1 = 5;
4) 0 ∙ 4 = 0 + 0 + 0 + 0 = 0;
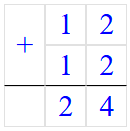
5) 12 ∙ 2 = 12 + 12 = 24;
Краткое условие: Вставь вместо кружка (О) один из этих знаков, чтобы равенство или неравенство стало верным.
4 ∙ 5 > 4 + 4 + 4 + 4, т.к.4 ∙ 5 > 4 ∙ 4;
6 + 6 + 6 + 6 + 6 = 6 ∙ 5, т.к. 6 ∙ 5 = 6 ∙ 5;
1 ∙ 3 < 1 + 1 + 1 + 1, т.к. 1 ∙ 3 < 1 ∙ 4.
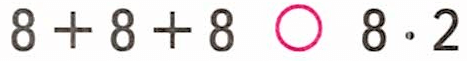
1. 8 ∙ 2 = 8 + 8;
2. Сумма 3-х восьмерок больше суммы 2-х восьмерок.
Поэтому 8 + 8 + 8 < 8 ∙ 2;
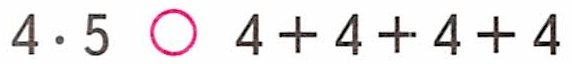
1. 4 ∙ 5 = 4 + 4 + 4 + 4 + 4;
2. Сумма 5-ти четверок больше суммы 4-х четверок.
Поэтому 4 ∙ 5 = 4 + 4 + 4 + 4;

1. 6 ∙ 5 = 6 + 6 + 6 + 6 + 6;
2. Сумма 5-ти шестерок равна сумме 5-ти шестерок.
Поэтому 6 + 6 + 6 + 6 + 6 = 6 ∙ 5;

1. 1 ∙ 3 = 1 + 1 + 1;
2. Сумма 3-х единиц меньше суммы 4-х единиц.
Поэтому 1 ∙ 3 < 1 + 1 + 1 + 1;
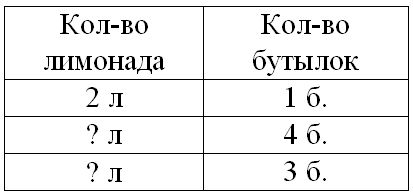
Краткое условие: В каждой бутылке по 2 л лимонада. Сколько литров лимонада в четырёх бутылках? в трёх?
В 4-х бутылках – ? л лимонада;
В 3-х бутылках – ? л лимонада.
2) 2 ∙ 3 = 6 (л) – лимонада в 3-х бутылках.
ШАГ 1. Найти сколько литров лимонада в четырёх бутылках.
ШАГ 2. Найти сколько литров лимонада в трёх бутылках.
2) Решим задачу:
1) 2 • 4 = 2 + 2 + 2 + 2 = 4 + 4 = 8 л – в 4 бутылках
Шаг 2. Найдём сколько литров лимонада в трёх бутылках:
2) 2 • 3 = 2 + 2 + 2 = 4 + 2 = 6 л – в 3 бутылках
2) 2 • 3 = 6 (л)
Ответ: в 3 бутылках 6 л лимонада; в 4 бутылках 8 л лимонада.
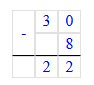
Краткое условие: В бидоне 30 л молока. Из него налили молоко в банки: в одну 5 л, в другую 3 л. Задай вопрос так, чтобы в задаче был ответ: 22 л. Реши задачу разными способами.
Вылили – 5 л и 3 л молока;
Осталось – ? л молока.
2) 30 - 8 = 22 (л) – молока осталось.
2) 25 - 3 = 22 (л) – молока осталось.
2) 27 - 5 = 22 (л) – молока осталось.
1 способ:
ШАГ 1. Найти сколько всего молока в банках.
ШАГ 2. Найти сколько молока осталось.
2 способ:
ШАГ 1. Найти сколько молока осталось сначала.
ШАГ 2. Найти сколько всего молока осталось.
В бидоне 30 л молока. Из него налили молоко в банки: в одну 5 л, в другую 3 л. Сколько литров молока осталось в бидоне?
2) Решим задачу разными способами:
Решая задачу первым способом, сначала необходимо найти количество молока, которое налили в банки, а потом то количество молока, которое осталось в бидоне.
Решая задачу вторым способом, необходимо сначала найти сколько молока осталось после того, как налили в банку 5 л, а потом сколько молока осталось в бидоне.

Шаг 1. Найдём сколько всего молока в банках:
1) 5 + 3 = 8 л – в банках
Шаг 2. Найдём сколько молока осталось:
2) 30 - 8 = 22 л – осталось
2 способ:
Шаг 1. Найдём сколько молока осталось сначала:
1) 30 - 5 = 25 л – осталось сначала
Шаг 2. Найдём сколько всего молока осталось:
2) 25 - 3 = 22 л – осталось всего
1) 5 + 3 = 8 (л)
2) 30 - 8 = 22 (л)
2 способ:
1) 30 - 5 = 25 (л)
2) 25 - 3 = 22 (л)
Ответ: в бидоне осталось 22 л молока.
Краткое условие: Длина одной стороны прямоугольника 4 см, другой — на 3 см меньше. Найди периметр этого прямоугольника.
2) (4 + 1) ∙ 2 = 5 ∙ 2 = 10 (см) – периметр прямоугольника.
ШАГ 1. Найти ширину прямоугольника.
ШАГ 2. Найти периметр прямоугольника.

1) 4 - 3 = 1 см – ширина прямоугольника
Шаг 2. Найдём периметр прямоугольника:
2) Р = (4 + 1) • 2 = 5 • 2 = 10 см – периметр прямоугольника
2) Р = (4 + 1) • 2 = 10 (см)
Ответ: периметр прямоугольника равен 10 см.
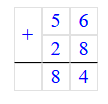
56 + 28 = 84;
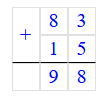
83 + 15 = 98;
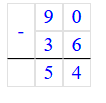
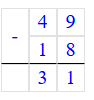
49 - 18 = 31.

2) 56 + 28 = 84;

3) 83 + 15 = 98;

4) 49 - 18 = 31;

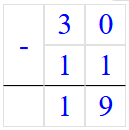
30 - (6 + 5) = 30 - 11 = 19;
7 + 53 = 60;
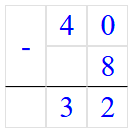
40 - 8 = 32;
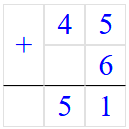
45 + 6 + 4 = 45 + (6 + 4) = 45 + 10 = 55;
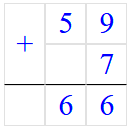
59 + 7 + 3 = 59 + (7 + 3) = 59 + 10 = 69.
ШАГ 1. Выполняем действия в скобках.
ШАГ 2. Выполняем сложение и вычитание по порядку.


4) 40 - 8 = 32;
Краткое условие: Сколько осей симметрии у этой фигуры?
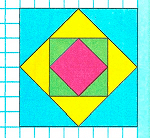
2) Начертим и раскрасим узор:

3) Подумаем, сколько осей симметрии у этой фигуры:
У данной фигуры четыре оси симметрии.
Краткое условие: На сколько больше лапок у 6 цыплят, чем ног у одной лошади?
ШАГ 1. Найти сколько лапок у 6 цыплят.
ШАГ 2. Найти на сколько больше лапок у 6 цыплят.

1) 2 • 6 = 2 + 2 + 2 + 2 + 2 + 2 = 12 л. – у 6 цыплят
Шаг 2. Найдём на сколько больше лапок у 6 цыплят:
2) 12 - 4 = 8 л. – на столько лапок больше
2) 12 - 4 = 8 (л.)
Ответ: у 6 цыплят на 8 лапок больше, чем ног у 1 лошади.



