Часть 1 страница 65, ГДЗ по математике за 2 класс к учебнику Моро, Бантовой, Бельтюковой Школа России
Страница 65
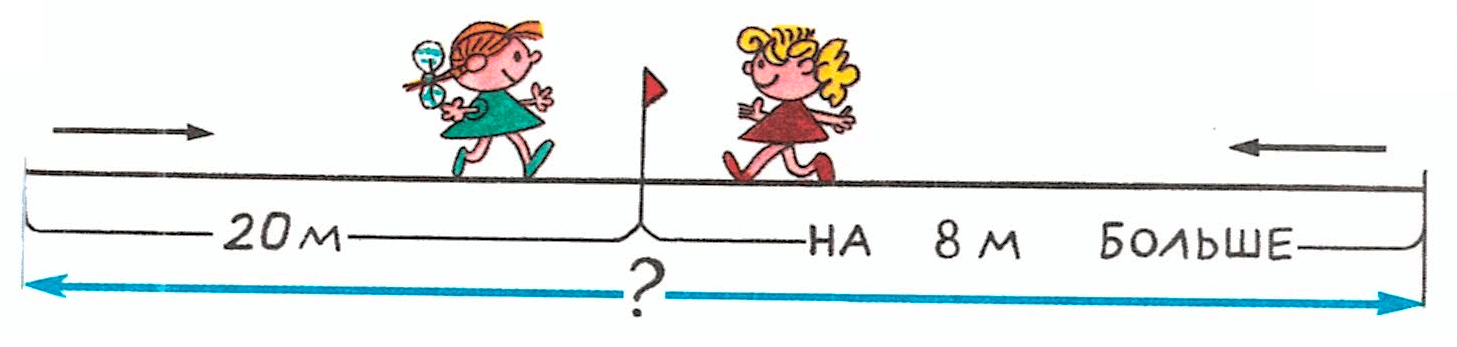
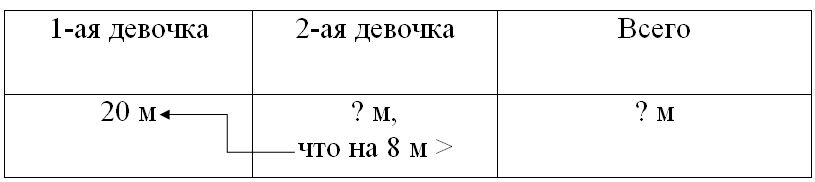
Краткое условие: Две девочки измеряли длину дорожки с двух концов, идя навстречу друг другу. Одна девочка прошла до встречи 20 м, другая — на 8 м больше. Какой длины была эта дорожка?
2) 20 + 28 = 48 (м) – длина дорожки.
ШАГ 1. Найти сколько метров прошла до встречи вторая девочка.
ШАГ 2. Найти длину дорожки.
2) Решим задачу:
1) 20 + 8 = 28 м – прошла вторая девочка
Шаг 2. Найдём длину дорожки:
2) 20 + 28 = 48 м – всего
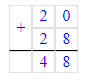
2) 20 + 28 = 48 (м)
Ответ: длина дорожки равна 48 м.
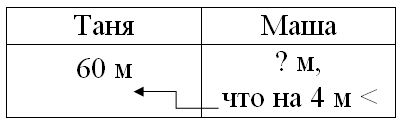
Краткое условие: Таня и Маша бежали наперегонки. Когда Таня пробежала 60 м, Маша отстала от неё на 4 м. Сколько метров пробежала Маша? Сделай схематический чертёж и реши задачу.
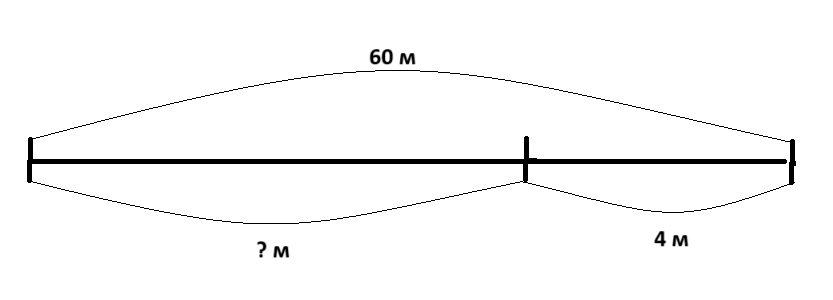
ШАГ 1. Найти сколько метров пробежала Маша.
2) Решим задачу:
1) 60 – 4 = 56 м – пробежала Маша
Ответ: Маша пробежала 56 метров.
Краткое условие: Сколько кубов на рисунке?
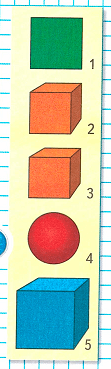
2) Подумаем, сколько кубов на рисунке:
1 – это квадрат;
2 – это куб;
3 – это куб;
4 – это круг;
5 – это куб;
Следовательно, всего на рисунке три куба.
Краткое условие: В одной корзине 6 кг яблок, в другой — 8 кг, а в ящике 10 кг яблок. На сколько килограммов яблок больше в двух корзинах, чем в ящике?
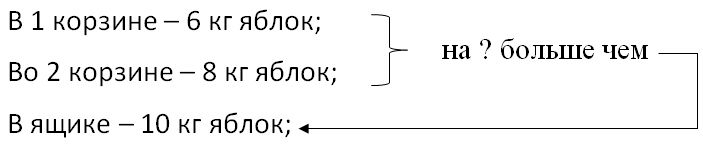
2) 14 - 10 = на 4 (кг) – яблок больше в корзинах, чем в ящике.
ШАГ 1. Найти сколько яблок в двух корзинах.
ШАГ 2. Найти на сколько килограммов яблок больше в двух корзинах, чем в ящике.
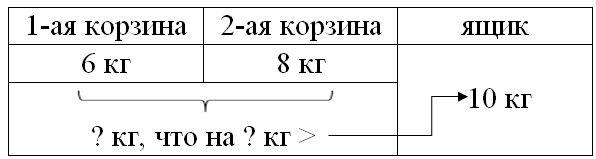
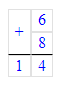
1) 6 + 8 = 14 кг – столько яблок в двух корзинах
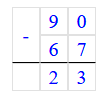
2) 14 - 10 = 4 кг – на столько больше
2) 14 - 10 = 4 (кг)
Ответ: в двух корзинах на 4 кг яблок больше, чем в ящике.
40 + 50 - 67 = 90 - 67 = 23;
30 + 18 - 20 = 48 - 20 = 28;
90 - (80 - 60) = 90 - 20 = 70;
70 - (32 + 8) = 70 - 40 = 30;
60 - (47 - 7) = 60 - 40 = 20;
75 + 25 - 9 = 100 - 9 = 91;
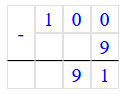
83 + 17 - 5 = 100 - 5 = 95;
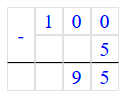
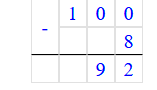
64 + 36 - 8 = 100 - 8 = 92.
ШАГ 1. Выполняем действия в скобках.
ШАГ 2. Выполняем сложение и вычитание по порядку.
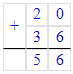
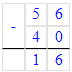



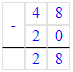
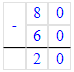

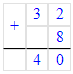


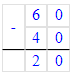






8 + 4 = 12;
13 - 7 = 6;
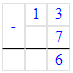
17 - 8 = 9;
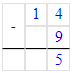
14 - 9 = 5;
11 - 8 = 3.
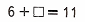
6 + 5 = 11;

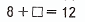
8 + 4 = 12;

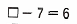
13 – 7 = 6;
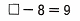
17 – 8 = 9;

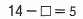
14 – 9 = 5;
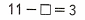
11 – 8 = 3;
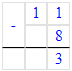
Краткое условие: Сравни выражения.
7 + 32 = 32 + 7, т.к. 39 = 39;
88 - 7 < 98 - 7, т.к. 81 < 91;
79 - 6 < 97 - 7, т.к. 73 < 90.
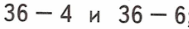
1. 36 – 4 = 32;
2. 36 – 6 = 30;
Так как 32 > 30, то 36 – 4 > 36 – 6;
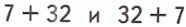
1. 7 + 32 = 39;

2. 32 + 7 = 39;
Так как 39 = 39, то 7 + 32 = 32 + 7;
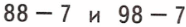
1. 88 – 7 = 81;
2. 98 – 7 = 91;
Так как 81 < 91, то 88 – 7 < 98 – 7;

1. 79 – 6 = 73;
2. 97 – 7 = 90;
Так как 73 < 90, то 79 – 6 < 97 – 7;
Краткое условие: Сложи числа в каждом квадрате по строкам, по столбцам, из угла в угол. Если суммы равны, то такой квадрат называется магическим.
Квадрат магический.
В розовом квадрате: 5 + 0 + 7 = 6 + 4 + 2 = 1 + 8 + 3 = 5 + 6 + 1 = 0 + 4 + 8 = 7 + 2 + 3 = 5 + 4 + 3 = 7 + 4 + 1 = 12.
Квадрат магический.
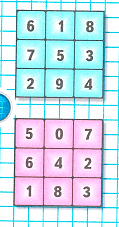
2) Подумаем, является ли первый квадрат магическим:
1. 6 + 1 + 8 = 7 + 8 = 15

2. 7 + 5 + 3 = 10 + 5 = 15;
3. 2 + 9 + 4 = 6 + 9 = 15;

4. 6 + 7 + 2 = 8 + 7 = 15;

5. 1 + 5 + 9 = 10 + 5 = 15;
6. 8 + 3 + 4 = 8 + 7 = 15;
7. 6 + 5 + 4 = 11 + 4 = 15;
8. 8 + 5 + 2 = 10 + 5 = 15;
Так как суммы по строкам, столбцам и из угла в угол равны, следовательно, что квадрат является магическим.
3) Подумаем, является ли второй квадрат магическим:
1. 5 + 0 + 7 = 5 + 7 = 12;
2. 6 + 4 + 2 = 10 + 2 = 12;
3. 1 + 8 + 3 = 9 + 3 = 12;

4. 5 + 6 + 1 = 11 + 1 = 12;
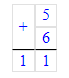
5. 0 + 4 + 8 = 4 + 8 = 12;
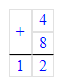
6. 7 + 2 + 3 = 9 + 3 = 12;

7. 5 + 4 + 3 = 9 + 3 = 12;

8. 7 + 4 + 1 = 11 + 1 = 12;

Так как суммы по строкам, столбцам и из угла в угол равны, следовательно, что квадрат является магическим.
1. 17;
17 + 3 = 20;
2. 19;
19 + 1 = 20;
3. 18;
18 + 2 = 20;
4. 16;
16 + 4 = 20;
5. 15;
15 + 5 = 20;
2) Дополним до 50 числа:
1. 44;
44 + 6 = 50;
2. 48;
48 + 2 = 50;
3. 49;
49 + 1 = 50;
4. 46;
46 + 4 = 50;
5. 45;
45 + 5 = 50;



