Часть 1 страница 42, ГДЗ по математике за 2 класс к учебнику Моро, Бантовой, Бельтюковой Школа России

Краткое условие: 1) Измерь стороны многоугольников и найди периметр каждого из них в сантиметрах. 2) Вспомни, как, используя циркуль, находили длину ломаной. Расскажи, как можно найти периметр многоугольника, не узнавая длину каждой из его сторон. Найди этим способом периметр треугольника.

Краткое решение Подробное решение

Решение:

1) Фигура 1: 3 + 4 + 1 + 4 = 12 (см).
Фигура 2: 3 + 3 + 4 = 10 (см).
Фигура 3: 2 + 5 + 5 + 3 = 15 (см).
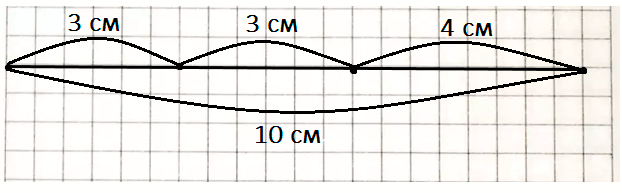
2) На прямой отложить отрезки, равные по длине сторонам треугольника. Затем, с помощью линейки измерить длину получившегося отрезка:

Решение:

1) Рассмотрим многоугольники:

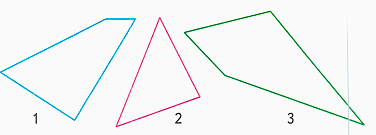
2) Измерим стороны многоугольников и найдем периметр каждого из них в сантиметрах:
1. Р = 3 см + 4 см + 1 см + 4 см = 7 см + 5 см = 12 см;

2. Р = 4 см + 3 см + 3 см = 7 см + 3 см = 10 см;
3. Р = 2 см + 3 см + 5 см + 5 см = 5 см + 10 см = 15 см;
3) Вспомним, как, используя циркуль, найти длину ломаной и данных многоугольников:
Чтобы найти длину ломаных с помощью циркуля, необходимо начертить прямую, отложить на ней отрезки, вымеренные с помощью циркуля и равные по длине сторонам ломаной. Далее нужно измерить длину всего получившегося отрезка – это и будет длина ломаной.
4) Найдем этим способом периметр треугольника:

Ответ:

периметр первого многоугольника равен 12 см; периметр второго многоугольника равен 10 см; периметр третьего многоугольника равен 15 см.

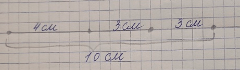
Краткое условие: Слава согнул кусок проволоки так, что получился треугольник со сторонами длиной 8 см, 3 см и 6 см. Какой длины был этот кусок проволоки? Чему равен периметр треугольника?

Краткое решение Подробное решение

Дано:

1 сторона – 8 см;
2 сторона – 3 см;
3 сторона – 6 см
Периметр – ?

Решение:

1) 8 + 3 + 6 = 17 (см) – периметр треугольника или длина проволоки.

Ответ:

17 см.

Подсказка

Чтобы решить задачу, нужно:
ШАГ 1. Найти какой длины был кусок проволоки и чему равен периметр треугольника.

Дано:

Решение:

Шаг 1. Найдём какой длины был кусок проволоки и чему равен периметр треугольника:
1) Р = 8 см + 3 см + 6 см = 11 см + 6 см = 17 см – периметр треугольника и длина проволоки

Ответ:

кусок проволоки был 17 см, а значит, это и был периметр треугольника.

Под запись в тетрадь:

1) Р = 8 см + 3 см + 6 см = 17 см;
Ответ: кусок проволоки был 17 см, а значит, это и был периметр треугольника.

Краткое условие: Сравни выражения. 1) Сумму чисел 8 и 9 и разность чисел 20 и 1. 2) Разность чисел 16 и 8 и разность чисел 16 и 10.

Краткое решение Подробное решение

Решение:

1) 8 + 9 < 20 - 1, т.к. 17 < 19.
2) 16 - 8 > 16 - 10, т.к. 8 > 6.

Решение:

Сравним выражения:
1) Сумму чисел 8 и 9 и разность чисел 20 и 1.
8 + 9 = 17;

20 – 1 = 19;
Так как 17 < 19, то 8 + 9 < 20 – 1;
2) Разность чисел 16 и 8 и разность чисел 16 и 10.
16 - 8 = 8;

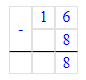
16 – 10 = 6;
Так как 8 > 6, то 16 - 8 > 16 – 10;

Краткое условие: У Димы две монеты: 5 р. и 2 р. Он купил тетрадь за 3 р. Сколько рублей у него осталось? Юля и Слава составили по этой задаче разные выражения. Объясни, как рассуждал каждый из них.

Краткое решение Подробное решение

Дано:

У Димы – 5 р. и 2 р.;
Купил тетрадь за 3 р.;
Осталось – ? р.

Решение:

Юля рассуждала:(5 + 2) - 3, т.е.
1) 5 + 2 = 7 (р.) – всего было у Димы;
2) 7 - 3 = 4 (р.) – у Димы осталось, после покупки.
Слава рассуждал: (5 - 3) + 2, т.е.
1) 5 - 3 = 2 (р.) – дал сдачи продавец Диме, после покупки тетради монетой в 5 рублей;
2) 2 + 2 = 4(р.) – у Димы осталось, после покупки.

Ответ:

4 рубля.

Решение:

1) Рассмотрим выражения для решения задачи:

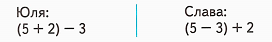
2) Объясним, как рассуждал каждый из ребят при условии, что у Димы две монеты: 5 р. и 2 р., при этом он купил тетрадь за 3 р.:
1. При решении задачи Юля сначала нашла общее количество денег, которое было у Димы, а после сколько рублей осталось после покупки тетради.
2. При решении задачи Слава сначала нашёл сколько рублей от 5 р. осталось после покупки тетради, а после сколько рублей стало с учётом монеты в 2 р.